题目内容
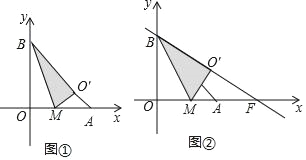
【题目】将一个直角三角形纸片ABO,放置在平面直角坐标系中,点A(2,0),点B(0,2),点O(0,0).点M为边OA上的一个动点(点M不与点O、A重合),沿着BM折叠该纸片,得顶点O的对应点O′.
(I)如图①,当点O′在边AB上时,求点O′的坐标;
(II)设直线BO′与x轴相交于点F.
①如图②,当BA平分∠MBF时,求点F的坐标;
②当OM=![]() 时,求点F的坐标(直接写出结果即可)
时,求点F的坐标(直接写出结果即可)
【答案】(Ⅰ)O'(![]() ,2﹣
,2﹣![]() );(Ⅱ)①F(2
);(Ⅱ)①F(2![]() ,0);②F(
,0);②F(![]() ,0)
,0)
【解析】
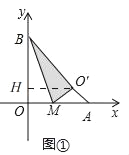
(I) 过点O'作O'H⊥y轴于H,由折叠可知,BO'=BO=2,∠BO'H=∠BAO=45°,利用特殊角的三角函数值求出BH、O'H,从而得到O'的坐标;
(II) ①由BA平分∠MBF时,得到∠OBF=60,利用特殊角的三角函数值求出OF,即可得到点F的坐标;②先说明△FO'M∽△FOB,从而![]() =
=![]() ,设F(a,0),利用勾股定理,用含a式子表示O'F,代入
,设F(a,0),利用勾股定理,用含a式子表示O'F,代入![]() =
=![]() ,求出a,从而得到点F的坐标.
,求出a,从而得到点F的坐标.
解:(I)如图①,过点O'作O'H⊥y轴于H,
由折叠知,△BMO≌△BMO',
∴BO'=BO=2,
∵O'H∥OA,
∴∠BO'H=∠BAO=45°,
在Rt△BO'H中,O'H=BO'cos∠BO'H=![]() ,
,
∴BH=O'H=![]() ,
,
∴OH=OB﹣BH=2﹣![]() ,
,
∴O'(![]() ,2﹣
,2﹣![]() );
);
(II)①∵BA平分∠MBF,
∴∠ABO=3∠MBA=45°,
∴∠ABF=∠MBA=15°,
∴∠OBF=∠ABO+∠ABF=60°,
在Rt△BOF中,OF=OBtan60=2![]() ,
,
∴F(2![]() ,0);
,0);
②由折叠知,O'M=OM=![]() ,O'B=OB=2,∠MO'F=90°=∠FOB,
,O'B=OB=2,∠MO'F=90°=∠FOB,
∵∠FO'M=∠FOB,
∴△FO'M∽△FOB,
∴![]() =
=![]() ,
,
设F(a,0)(a>0),
∴OF=a,
在Rt△BOF中,BF=![]() ,
,
∴O'F=![]() ﹣2,
﹣2,
∴![]() ,
,
∴a=0(舍)或a=![]() ,
,
F(![]() ,0).
,0).
故答案为:(I)O'(![]() ,2﹣
,2﹣![]() );(II)①F(2
);(II)①F(2![]() ,0);②F(
,0);②F(![]() ,0)
,0)

 快乐5加2金卷系列答案
快乐5加2金卷系列答案