题目内容
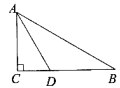
【题目】如图,在Rt△ABC中,∠ACB=90°,∠B=30°,AD为∠CAB的角平分线,若CD=3，则DB=____.
【答案】6
【解析】
先根据三角形的内角和定理，求出∠BAC的度数=180°﹣90°﹣30°=60°，然后利用角平分线的性质，求出∠CAD的度数
∠BAC=30°．在Rt△ACD中，根据30°角所对的直角边等于斜边的一半，即可求出AD的长，进而得出BD．
在Rt△ABC中∠C=90°，∠B=30°，∴∠BAC=180°﹣90°﹣30°=60°．
∵AD是角平分线，∴∠BAD=∠CAD∠BAC=30°．在Rt△ACD中，∵∠CAD=30°，CD=3，∴AD=6．
∵∠B=∠BAD=30°，∴BD=AD=6．
故答案为：6．
练习册系列答案
阅读快车系列答案
相关题目
【题目】某校组织甲、乙两队开展“保护生态环境知识竞赛”，满分为10分，得分均为整数，规定得分达到6分及以上为合格，达到9分及以上为优秀，如图是甲、乙两队学生这次竞赛成绩分布条形统计图．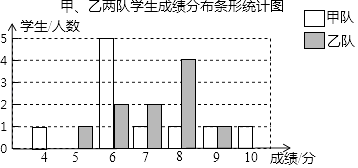
根据以上信息，请解答下面的问题：
（1）在下面甲、乙两队的成绩统计表中，a= ， b=c= ．
平均分 | 中位数 | 众数 | 方差 | 合格率 | 优秀率 | |
甲队 | a | 6 | c | 2.76 | 90% | 20% |
乙队 | 7.2 | b | 8 | 1.36 | 80% | 10% |
（2）小华同学说：“我在这次比赛中得到了7分，这在我所在的小队成绩中属于中等偏上的位置！”观察（1）中的表格，小华是队的学生；（填“甲”或“乙”）
（3）甲队同学认为：甲队的合格率、优秀率均高于乙队，所以甲队的成绩好于乙队．但乙队同学不同意甲队同学的说法，认为乙队的成绩要好于甲队．请你写出两条支持乙队同学观点的理由．
（4）学校要从从甲、乙两队获得优秀的学生中，选取两名同学参加市级比赛，则恰好同时选中的两人均为甲队学生的概率为 ．
