题目内容
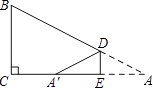
【题目】如图,ABCD的对角线AC、BD交于点O,AE平分∠BAD交BC于点E,且∠ADC=60°,AB= ![]() BC,连接OE.下列结论:①∠CAD=30°;②SABCD=ABAC;③OB=AB;④OE=
BC,连接OE.下列结论:①∠CAD=30°;②SABCD=ABAC;③OB=AB;④OE= ![]() BC,成立的个数有( )
BC,成立的个数有( )
A.1个
B.2个
C.3个
D.4个
【答案】C
【解析】解:∵四边形ABCD是平行四边形,
∴∠ABC=∠ADC=60°,∠BAD=120°,
∵AE平分∠BAD,
∴∠BAE=∠EAD=60°
∴△ABE是等边三角形,
∴AE=AB=BE,
∵AB= ![]() BC,
BC,
∴AE= ![]() BC,
BC,
∴∠BAC=90°,
∴∠CAD=30°,故①正确;
∵AC⊥AB,
∴SABCD=ABAC,故②正确,
∵AB= ![]() BC,OB=
BC,OB= ![]() BD,
BD,
∵BD>BC,
∴AB≠OB,故③错误;
∵CE=BE,CO=OA,
∴OE= ![]() AB,
AB,
∴OE= ![]() BC,故④正确.
BC,故④正确.
故C符合题意.
故答案为:C.
解答此题的关键是掌握平行四边形的性质和证得△ABE是等边三角形.在平行四边形的性质易得△ABE是等边三角形,又由![]() ,证得①;继而证得AC⊥AB,得到②;可得OE是△ABC的中位线,从而得到
,证得①;继而证得AC⊥AB,得到②;可得OE是△ABC的中位线,从而得到![]() ,可证得④.由
,可证得④.由![]() ,
,![]() ,BD>BC,可得AB≠OB可得③错误.
,BD>BC,可得AB≠OB可得③错误.

练习册系列答案
相关题目