题目内容
【题目】如图,将一矩形OABC放在直角坐标系中,O为坐标原点,点A在y轴正半轴上,点E是边AB上的一个动点(不与点A、B重合),过点E的反比例函数y= ![]() (x>0)的图象与边BC交与点F.
(x>0)的图象与边BC交与点F.
(1)若△OAE、△OCF的面积分别为S1、S2 , 且S1+S2=2,求k的值;
(2)在(1)的结论下,当OA=2,OC=4时,求三角形OEF的面积.
【答案】
(1)∵点E、F在函数y= ![]() (x>0)的图象上,
(x>0)的图象上, 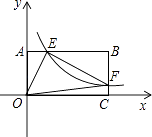
∴设E(x1, ![]() )(x1>0),F(x2,
)(x1>0),F(x2, ![]() )(x2>0),
)(x2>0),
∴S1= ![]() x1
x1 ![]() =
= ![]() ,S2=
,S2= ![]() x2
x2 ![]() =
= ![]() ,
,
∵S1+S2=2,
∴ ![]() +
+ ![]() =2,
=2,
∴k=2;
(2)解:∵四边形OABC为矩形,OA=2,OC=4,
∴E(1,2),F(4, ![]() ),
),
∴AE=1,BE=3,BF= ![]() ,CF=
,CF= ![]() ,
,
∴S△OEF=S矩形AOCE﹣S△AOE﹣S△OCF﹣S△BEF= ![]() .
.
【解析】(1)利用反比例函数图像上点的坐标特点设出E、F的坐标,分别表示出S1、S2,再由S1+S2=2即可得k的值;
(2)根据矩形的性质求出E、F的坐标,再根据S△OEF=S矩形AOCE﹣S△AOE﹣S△OCF﹣S△BEF可求出结果.

练习册系列答案
相关题目
【题目】某公司有A、B两种型号的客车共11辆,它们的载客量(不含司机)、日租金、车辆数如下表所示,已知这11辆客车满载时可搭载乘客350人.
A型客车 | B型客车 | |
载客量(人/辆) | 40 | 25 |
日租金(元/辆) | 320 | 200 |
车辆数(辆) | a | b |
(1)求a、b的值;
(2)某校七年级师生周日集体参加社会实践,计划租用A、B两种型号的客车共6辆,且租车总费用不超过1700元.
①最多能租用A型客车多少辆?
②若七年级师生共195人,写出所有的租车方案,并确定最省钱的租车方案.