题目内容
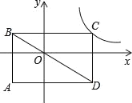
【题目】如图①,等腰Rt△ABC中,∠C=90o,D是AB的中点,Rt△DEF的两条直角边DE、DF分别与AC、BC相交于点M、N.
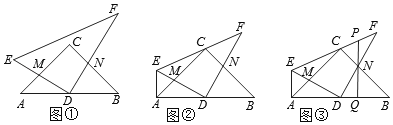
(1)思考推证:CM+CN=BC;
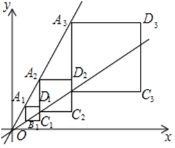
(2)探究证明:如图②,若EF经过点C,AE⊥AB,判断线段MA、ME、MC、DN四条线段之间的数量关系,并证明你的结论;
(3)拓展应用:如图③,在②的条件下,若AB=4,AE=1,Q为线段DB上一点,DQ=![]() ,QN的延长线交EF于点P,求线段PQ的长.
,QN的延长线交EF于点P,求线段PQ的长.
【答案】(1)详见解析;(2)![]() ,证明详见解析;(3)
,证明详见解析;(3)![]() .
.
【解析】
(1)如图1,连接CD.证明△BDN≌△CDM,即可解决问题;
(2)结论:![]() .利用相似三角形的性质即可解答.
.利用相似三角形的性质即可解答.
(3)如图3,连接CD,作EH⊥CD于H,证明△PNC≌△EAM,求出PN、QN的值即可解决问题.
(1)证明:连接CD,
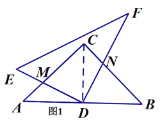

∵∠ACB=90,CA=CB,AD=DB,∴CD=AD=DB=![]() AB,
AB,
∠A=∠B=∠ACD=∠BCD=45,CD⊥AB,
∴∠CDN+∠BDN=90,
∵∠EDF=90,∴∠CDN+CDM=90,∴∠BDN=∠CDM,
∴△BDN≌△CDM, ∴BN=CM,
∴ BC=BN+CN=CM+CN;
(2)∵AE⊥AB,CD⊥AB,∴AE∥CD
∴△AEM∽△CDM,∴![]() ,
,
∵△BDN≌△CDM,∴DN=DM,
∴![]() ,即
,即![]() ;
;
(3)∵∠EDF=90,∴∠NDQ+∠ADE=90
∵EA⊥AD,∴∠AED+∠ADE=90 ,∴∠AED=∠NDQ
而AE=1,AD=CD=DB=![]() AB=2,∴ED=
AB=2,∴ED=![]()
∵△AEM∽△CDM,∴![]() ,∴DM=DN=
,∴DM=DN=![]() ED=
ED=![]() ,
,
而DQ=![]() ,∴
,∴![]() ,
,
∴△AED∽△QDN,![]()
过点E作EH⊥CD于点H,∴DH=AE=1,EH=AD=2,∴CH=2-1=1,

∴EC=![]() ,∴EC=ED,∴∠ECD=∠EDC=∠AEM,
,∴EC=ED,∴∠ECD=∠EDC=∠AEM,
∵PQ⊥AB,∴∠B=∠BNQ=∠PNC=45,
而∠PCN+∠NCD+∠ECD=∠EMA+∠AEM+∠EAM=180,
∠PCN=∠AME,而∠EAM=∠PNC=45,CN=AM,
∴△PNC≌△EAM,∴PN=AE=1,
∴![]() .
.

 习题精选系列答案
习题精选系列答案【题目】某校在争创“全国文明城市”活动中,组织全体学生参加了“创文”知识竞赛,为了解各年级成绩情况,学校这样做的:
(收集数据)从七、八、九三个年级的竞赛成绩中各随机抽取了10名学生成绩如下表:
七年级 | 60 | 70 | 60 | 100 | 80 | 70 | 80 | 60 | 40 | 90 |
八年级 | 80 | 80 | 100 | 40 | 70 | 60 | 80 | 90 | 50 | 80 |
九年级 | 70 | 50 | 60 | 90 | 100 | 80 | 80 | 90 | 70 | 70 |
(整理、描述数据)(说明:80≤x≤100为优秀,60≤x<80为合格,40≤x<60为一般)
年级 | 40≤x<60 | 60≤x<80 | 80≤x≤100 |
七年级 | 1 | 5 | 4 |
八年级 | 2 | 2 | 6 |
九年级 | 1 | 4 | 5 |
年级 | 平均数 | 众数 | 中位数 |
七年级 | a | 60 | 70 |
八年级 | 73 | b | 80 |
九年级 | 76 | 70 | c |
(分析数据)三组样本数据的平均分、众数、中位数如上表所示,其中a= ,b= ,c= .
(得出结论)请你根据以上信息,推断你认为成绩好的年级,并说明理由(至少从两个角度说明)