题目内容
【题目】某校在争创“全国文明城市”活动中,组织全体学生参加了“创文”知识竞赛,为了解各年级成绩情况,学校这样做的:
(收集数据)从七、八、九三个年级的竞赛成绩中各随机抽取了10名学生成绩如下表:
七年级 | 60 | 70 | 60 | 100 | 80 | 70 | 80 | 60 | 40 | 90 |
八年级 | 80 | 80 | 100 | 40 | 70 | 60 | 80 | 90 | 50 | 80 |
九年级 | 70 | 50 | 60 | 90 | 100 | 80 | 80 | 90 | 70 | 70 |
(整理、描述数据)(说明:80≤x≤100为优秀,60≤x<80为合格,40≤x<60为一般)
年级 | 40≤x<60 | 60≤x<80 | 80≤x≤100 |
七年级 | 1 | 5 | 4 |
八年级 | 2 | 2 | 6 |
九年级 | 1 | 4 | 5 |
年级 | 平均数 | 众数 | 中位数 |
七年级 | a | 60 | 70 |
八年级 | 73 | b | 80 |
九年级 | 76 | 70 | c |
(分析数据)三组样本数据的平均分、众数、中位数如上表所示,其中a= ,b= ,c= .
(得出结论)请你根据以上信息,推断你认为成绩好的年级,并说明理由(至少从两个角度说明)
【答案】(1)![]() ,
,![]() ,
,![]() ; (2)九年级的成绩好,理由详见解析.
; (2)九年级的成绩好,理由详见解析.
【解析】
(1)根据10名学生成绩表可得出平均数、众数和中位数即可解答;
(2)根据平均分高和成绩一般的人少分析判断即可解答.
(1)根据成绩表可得,![]() ,
,![]() ,
,![]() ;
;
(2)我认为九年级的成绩好,因为九年级成绩一般的人数最少,平均分最高.

 举一反三期末百分冲刺卷系列答案
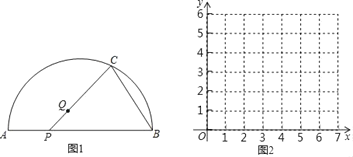
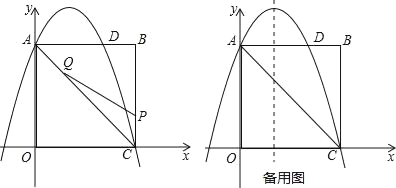
举一反三期末百分冲刺卷系列答案【题目】如图,点P是![]() 所对弦AB上一动点,点Q是
所对弦AB上一动点,点Q是![]() 与弦AB所围成的图形的内部的一定点,作射线PQ交
与弦AB所围成的图形的内部的一定点,作射线PQ交![]() 于点C,连接BC.已知AB=6cm,设A,P两点间的距离为xcm,P,C两点间的距离为y1cm,B,C两点间的距离为y2cm.(当点P与点A重合时,x的值为0).
于点C,连接BC.已知AB=6cm,设A,P两点间的距离为xcm,P,C两点间的距离为y1cm,B,C两点间的距离为y2cm.(当点P与点A重合时,x的值为0).
小平根据学习函数的经验,分别对函数y1,y2随自变量x的变化而变化的规律进行了探究.
下面是小平的探究过程,请补充完整:
(1)按照下表中自变量x的值进行取点、画图、测量,分别得到了y与x的几组对应值;
x/cm | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
y1/cm | 5.37 | 4.06 | 2.83 | m | 3.86 | 4.83 | 5.82 |
y2/cm | 2.68 | 3.57 | 4.90 | 5.54 | 5.72 | 5.79 | 5.82 |
经测量m的值是(保留一位小数).
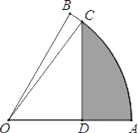
(2)在同一平面直角坐标系xOy中,描出补全后的表中各组数值所对应的点(x,y1),(x,y2),并画出函数y1,y2的图象;
(3)结合函数图象,解决问题:当△BCP为等腰三角形时,AP的长度约为 cm.