��Ŀ����
����Ŀ�����ߵ�����Ů��������е�һ��������Ŀ������������ɸߡ�������ƽ�иܼ�����֧����ɣ��˶�Ա�ɸ����Լ������ߺ�ϰ���ڹ涨��Χ�ڵ��ڸߡ������ܼ�ľ��룮ij��ȤС����ݸߵ����ĵ�һ�ֽ���ͼ������������ѧ���⣬������
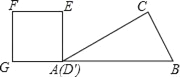
��ͼ��ʾ��������A��B�����ľ���Ϊ90cm�����ϵ�C��ֱ��AB�ľ���CE�ij�Ϊ155cm���߸��ϵ�D��ֱ��AB�ľ���DF�ij�Ϊ234cm����֪�ܵ�֧��AC��ֱ��AB�ļнǡ�CAEΪ82.4�����߸ܵ�֧��BD��ֱ��AB�ļнǡ�DBFΪ80.3������ߡ��ܼ��ˮƽ����CH�ij����������ȷ��1cm���ο�����sin82.4���0.991��cos82.4���0.132��tan82.4���7.500��sin80.3���0.983��cos80.3���0.168��tan80.3���5.850��

���𰸡��ߡ��ܼ��ˮƽ����CH�ij�Ϊ151cm��
������������������Ǻ�������Rt��ACE��Rt��DBF�У��ֱ����AE��BF�ij��������EF��ͨ������CEFH�õ�CH�ij���
��Rt��ACE��
��tan��CAE=![]() ��
��
��AE=![]()
��Rt��DBF��
��tan��DBF=![]() ��
��
��BF=![]() .
.
��EF=EA+AB+BF��21+90+40=151��cm��
��CE��EF��CH��DF��DF��EF
���ı���CEFH�Ǿ��Σ�
��CH=EF=151��cm��.
�𣺸ߡ��ܼ��ˮƽ����CH�ij�Ϊ151cm��

 100�ִ�����ĩ���ϵ�д�
100�ִ�����ĩ���ϵ�д� ��У���˿��ֿ���ϵ�д�
��У���˿��ֿ���ϵ�д�