Question

【题目】如图，Rt△AOB中，∠AOB=90°，OA在x轴上，OB在y轴上，点A，B的坐标分别为（ ，0），（0，1），把Rt△AOB沿着AB对折得到Rt△AO′B，则点O′的坐标为 ．

Answer 1

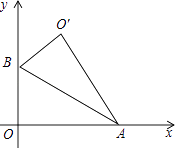
【答案】（ ， ）
【解析】解：如图，作O′C⊥y轴于点C， ∵点A，B的坐标分别为（ ，0），（0，1），
∴OB=1，OA= ，
∴tan∠BAO= = ，
∴∠BAO=30°，
∴∠OBA=60°，
∵Rt△AOB沿着AB对折得到Rt△AO′B，
∴∠CBO′=60°，
∴设BC=x，则OC′= x，
∴x2+（ x）2=1，
解得：x= （负值舍去），
∴O′C= ，
∴OC=OB+BC=1+ = ，
∴点O′的坐标为（ ， ）．
故答案为：（ ， ）．

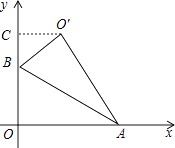
作O′C⊥y轴于点C，首先根据点A，B的坐标分别为（ ，0），（0，1）得到∠BAO=30°，从而得出∠OBA=60°，然后根据Rt△AOB沿着AB对折得到Rt△AO′B，得到∠CBO′=60°，最后设BC=x，则OC′= x，利用勾股定理求得x的值即可求解．