题目内容
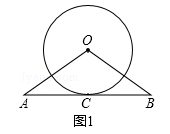
【题目】如图,数轴上点 A、B 到表示-2 的点的距离都为 6,P 为线段 AB 上任一点,C,D 两点分别从 P,B 同时向 A 点移动,且 C 点运动速度为每秒 2 个单位长度,D 点运动速度 为每秒 3 个单位长度,运动时间为 t 秒.
(1)A 点表示数为 ,B 点表示的数为 ,AB= .
(2)若 P 点表示的数是 0,
①运动 1 秒后,求 CD 的长度;
②当 D 在 BP 上运动时,求线段 AC、CD 之间的数量关系式.
(3)若 t=2 秒时,CD=1,请直接写出 P 点表示的数.
![]()
【答案】⑴-8;4;12;(2)见解析;(3)见解析.
【解析】
⑴根据点 A、B到表示-2 的点的距离都为6,列式即可求出A,B所表示的数,进而计算出AB的长度.
(2)①运动一秒后,C点为-2,D点为1,即可求出CD的长度.
②当点D在BP上运动时,分别用含![]() 的式子表示出AC=8-2t,CD=2t+4-3t=4-t,即可发现线段AC、CD之间的数量关系式.
的式子表示出AC=8-2t,CD=2t+4-3t=4-t,即可发现线段AC、CD之间的数量关系式.
(3)t=2秒时,D点为-2,根据CD=1,则C=-3或-1即可求出点P表示的数.
⑴![]()
故答案为:-8;4;12;
⑵①运动一秒后,C点为-2,D点为1,所以CD=3;
②当点D在BP上运动时,![]() ,此时C在线段AP上,AC=8-2t,
,此时C在线段AP上,AC=8-2t,
CD=2t+4-3t=4-t,所以AC=2CD;
⑶若 t=2秒时,D点为-2,若 CD=1,则 C=-3 或-1,
①当 C=-3 时,CP=4,此时 P=1;
②当 C=-1 时,P=3.

 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案【题目】水果市场将120吨水果运往各地商家,现有甲、乙、丙三种车型供选择,每辆车的运载能力和运费如下表所示:(假设每辆车均满载)
车型 | 甲 | 乙 | 丙 |
汽车运载量(吨/辆) | 5 | 8 | 10 |
汽车运费(元/辆) | 400 | 500 | 600 |
(1)若全部水果都用甲、乙两种车型来运送,需运费8200元,问分别需甲、乙两种车型各几辆?
(2)为了节约运费,市场可以调用甲、乙、丙三种车型参与运送(每种车型至少1辆),已知它们的总辆数为16辆,你能通过列方程组的方法分别求出几种车型的辆数吗?
【题目】小冬与小夏是某中学篮球队的队员,在最近五场球赛中的得分如下表所示:
第一场 | 第二场 | 第三场 | 第四场 | 第五场 | |
小冬 |
|
|
|
|
|
小夏 |
|
|
|
|
|
(1)根据上表所给的数据,填写下表:
平均数 | 中位数 | 众数 | 方差 | |
小冬 |
|
|
| |
小夏 |
|
|
|
(2)根据以上信息,若教练选择小冬参加下一场比赛,教练的理由是什么?
(3)若小冬的下一场球赛得分是![]() 分,则在小冬得分的四个统计量中(平均数、中位数、众数与方差)哪些发生了改变,改变后是变大还是变小?(只要回答是“变大”或“变小”)(
分,则在小冬得分的四个统计量中(平均数、中位数、众数与方差)哪些发生了改变,改变后是变大还是变小?(只要回答是“变大”或“变小”)(![]() )
)