题目内容
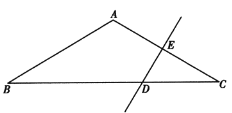
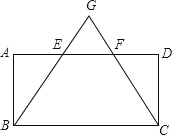
【题目】如图,在平行四边形ABCD中,E、F为AD上两点,AE=EF=FD,连接BE、CF并延长,交于点G, GB=GC.
(1)求证:四边形ABCD是矩形;
(2)若△GEF的面积为2.
①求四边形BCFE的面积;
②四边形ABCD的面积为 .
【答案】(1)证明见解析;(2)①16;②24;
【解析】
(1)根据平行四边形的性质得到AD∥BC,AB=DC,AB∥CD于是得到BE=CF,根据全等三角形的性质得到∠A=∠D,根据平行线的性质得到∠A+∠D=180°,由矩形的判定定理即可得到结论;
(2)①根据相似三角形的性质得到![]() ,求得△GBC的面积为18,于是得到四边形BCFE的面积为16;
,求得△GBC的面积为18,于是得到四边形BCFE的面积为16;
②根据四边形BCFE的面积为16,列方程得到BCAB=24,即可得到结论.
(1)证明:∵GB=GC,
∴∠GBC=∠GCB,
在平行四边形ABCD中,
∵AD∥BC,AB=DC,AB∥CD,
∴GB-GE=GC-GF,
∴BE=CF,
在△ABE与△DCF中,
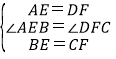 ,
,
∴△ABE≌△DCF,
∴∠A=∠D,
∵AB∥CD,
∴∠A+∠D=180°,
∴∠A=∠D=90°,
∴四边形ABCD是矩形;
(2)①∵EF∥BC,
∴△GFE∽△GBC,
∵EF=![]() AD,
AD,
∴EF=![]() BC,
BC,
∴![]() ,
,
∵△GEF的面积为2,
∴△GBC的面积为18,
∴四边形BCFE的面积为16,;
②∵四边形BCFE的面积为16,
∴![]() (EF+BC)AB=
(EF+BC)AB=![]() ×
×![]() BCAB=16,
BCAB=16,
∴BCAB=24,
∴四边形ABCD的面积为24,
故答案为:24.

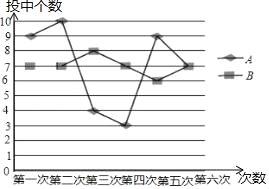
【题目】某班为确定参加学校投篮比赛的任选,在A、B两位投篮高手间进行了6次投篮比赛,每人每次投10个球,将他们每次投中的个数绘制成如图所示的折线统计图.
(1)根据图中所给信息填写下表:
投中个数统计 | 平均数 | 中位数 | 众数 |
A |
| 8 |
|
B | 7 |
| 7 |
(2)如果这个班只能在A、B之间选派一名学生参赛,从投篮稳定性考虑应该选派谁?请你利用学过的统计量对问题进行分析说明.