题目内容
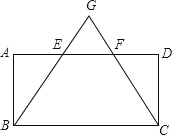
【题目】如图，在
中，
，
，点
是边
上的动点（点与点、
不重合），过点作
交射线
于点
，联结
，点
是的中点，过点 、作直线，交
于点
，联结
、
．
（1）当点在边上，设
,
．
①写出
关于
的函数关系式及定义域；
②判断
的形状，并给出证明；
（2）如果
，求
的长．
【答案】（1）①
；②详见解析；（2）
或
【解析】
（1）①先证△DEB为等腰直角三角形，设DB=x，CE=y知EB=
x，由EB+CE=4知x+y=4，从而得出答案；
②由∠ADE=90°，点F是AE的中点知CF=AF=
AE，DF=AF=AE，据此得出CF=DF，再由∠CFE=2∠CAE，∠EFD=2∠EAD知∠CFD=∠CFE+∠EFD=2∠CAE+2∠EAD=2∠CAD，结合∠CAB=45°知∠CFD=90°，据此可得答案；
（2）分点E在BC上和BC延长线上两种情况，分别求出DF、GF的长，从而得出答案．
(1)①∵
，
，
，
，
又
，
为等腰直角三角形，
，
，
，
又
，
，
；
②，，
，
点
是
的中点，
，
，
，∠CAF=∠ACF，∠EAD=∠FDA，
，
，
，
，
，
是等腰直角三角形；
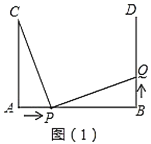
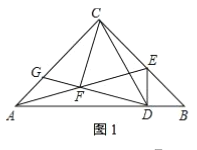
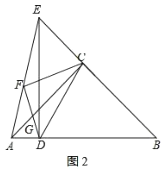
(2)如图
，当点
在
上时，
，
，
在
中，
，
则
，
∴sin∠CAE=
，
又
，
由（2）得：
，
∴∠CFG=90°，
∴
∴
，
；
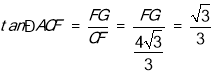
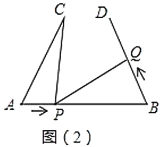
如图
，当点在延长线上时，，
同理可得，
在
中，，
，
综上所述：DG的长为或．
练习册系列答案
七彩题卡口算应用一点通系列答案
相关题目
【题目】今年3月，某集团随机抽取所属的m家商业连锁店进行评估，将各连锁店按照评估成绩分成了A、B、C、D四个等级，绘制了如图尚不完整的统计图表．
评估成绩 | 评定等级 | 频数 |
| A | 2 |
| B | b |
| C | 15 |
| D | 6 |
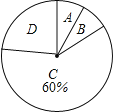
根据以上信息解答下列问题：
（1）求m，b的值；
（2）在扇形统计图中，求B等级所在扇形的圆心角的大小；
（3）从评估成绩不少于80分的连锁店中，任选2家介绍营销经验，用树状图或列表法求其中至少有一家是A等级的概率．
