题目内容
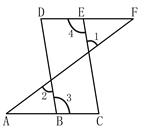
如图,点E在直线DF上,点B在直线AC上,若∠1=∠2,∠3=∠4,则∠A=∠F,请说明理由.
解:∵∠1=∠2(已知),∠2=∠DGF( )
∴∠1=∠DGF
∴BD∥CE( )
∴∠3+∠C=180º( )
又∵∠3=∠4(已知)
∴∠4+∠C=180º
∴ ∥ (同旁内角互补,两直线平行)
∴∠A=∠F( )
解:∵∠1=∠2(已知),∠2=∠DGF( )
∴∠1=∠DGF
∴BD∥CE( )
∴∠3+∠C=180º( )
又∵∠3=∠4(已知)
∴∠4+∠C=180º
∴ ∥ (同旁内角互补,两直线平行)
∴∠A=∠F( )

(对顶角相等)、(同位角相等,两直线平行)、(两直线平行,同旁内角互补)、DF、AC、(两直线平行,内错角相等)
试题分析:根据平行线的判定是由角的数量关系判断两直线的位置关系,平行线的性质是由平行关系来寻找角的数量关系,分别分析得出即可.
试题解析:∵∠1=∠2(已知)
∠2=∠DGF(对顶角相等),
∴∠1=∠DGF,
∴BD∥CE,(同位角相等,两直线平行),
∴∠3+∠C=180°,(两直线平行,同旁内角互补),
又∵∠3=∠4(已知)
∴∠4+∠C=180°
∴DF∥AC(同旁内角互补,两直线平行)
∴∠A=∠F(两直线平行,内错角相等).

练习册系列答案
相关题目
 ∥
∥ ,
, ,
, 平分
平分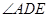 ,则
,则 的度数为 。
的度数为 。