题目内容
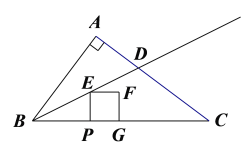
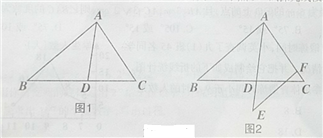
【题目】已知，如图1，AD是△ABC的角平分线，且AD=BD，
（1）求证：△CDA∽△CAB；
（2）若AD=6，CD=5，求AC的值；
（3）如图2，延长AD至E，使AE=AB，过E点作EF∥AB，交AC于点F，试探究线段EF
与线段AD的大小关系．
【答案】(1)证明见解析；（2）
【解析】试题分析：（1）根据角平分线的性质，得到∠BAD=∠CAD，再由等边对等角得到∠BAD=∠ABD，由等量代换得到∠CAD=∠B，即可得到结论；
（2）由相似三角形对应边成比例即可得到结论；
（3）结论为EF=AD．证明△BAD≌△EAF即可．
试题解析：（1）证明：∵AD是△ABC的角平分线，∴∠BAD=∠CAD．
∵AD=BD，∴∠BAD=∠ABD，∴∠CAD=∠B．∵∠C=∠C，∴△CDA∽△CAB．
（2）解：∵△CDA∽△CAB， ∴
，∴
，∴
，∴AC=．
（3）答：EF= AD．理由如下：
∵EF∥AB，∴∠E=∠BAD．∵∠BAD=∠B，∴∠B=∠E．
∵AE=AB，∠BAD=∠EAF，∴△BAD≌△EAF，∴EF= AD．
练习册系列答案
培优好卷单元加期末卷系列答案
相关题目
