题目内容
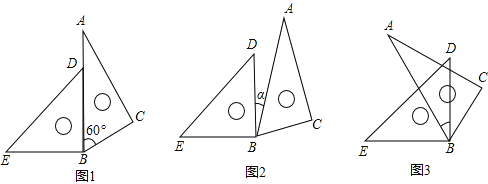
【题目】如图,在Rt△ABC中,∠BAC=90°,AB=6,AC=8.射线BD为∠ABC的平分线,交AC于点D.动点P以每秒2个单位长度的速度从点B向终点C运动.作PE⊥BC交射线BD于点E.以PE为边向右作正方形PEFG.正方形PEFG与△BDC重叠部分图形的面积为S.
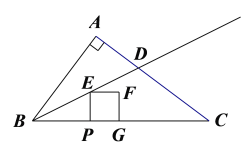
(1)求tan∠ABD的值.
(2)当点F落在AC边上时,求t的值.
(3)当正方形PEFG与△BDC重叠部分图形不是三角形时,求S与t之间的函数关系式.
【答案】(1)tan∠ABD=![]() ;(2)
;(2)![]() ;(3)①当
;(3)①当![]() 时,
时,![]() ;②当
;②当![]() 时,
时,![]() ;③当
;③当![]() 时,
时,![]() .
.
【解析】
(1)过点D作DH⊥BC于点H,可得△ABD≌△HBD,所以CH=BC-AB=4.再由三角形相似即可求出DH=AD=3.根据三角函数定义即可解题.
(2)由(1)得BP=2PE,所以BP=2t,PE=PG=EF=FG=t,当点F落在AC边上时,FG=![]() CG,即可得到方程求出t.
CG,即可得到方程求出t.
(3)当正方形PEFG与△BDC重叠部分图形不是三角形时,分三种情况分别求出S与t之间的函数关系式,①当![]() 时,F点在三角形内部或边上,②当
时,F点在三角形内部或边上,②当![]() 时,如图:E点在三角形内部,F点在外部,此时重叠部分图形的面积S=S正方形-S△FMN,③当
时,如图:E点在三角形内部,F点在外部,此时重叠部分图形的面积S=S正方形-S△FMN,③当![]() 时,重叠部分面积为梯形MPGN面积,
时,重叠部分面积为梯形MPGN面积,
解:(1)如图,在Rt△ABC中,∠BAC=90°,AB=6,AC=8
根据勾股定理得BC=10
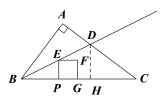
过点D作DH⊥BC于点H
∵△ABD≌△HBD,
∴BH=AH=6,DH=AD,
∴CH=4,
∵△ABC∽△HDC,
∴![]() ,
,
∴![]() ,
,
∴DH=AD=3,
∴tan∠ABD=![]() =
=![]() ,
,
(2)由(1)可知BP=2PE,依题意得:BP=2t,PE=PG=EF=FG=t,CG=10-3t,

当点F落在AC边上时,FG=![]() CG,
CG,
即![]() ,
,
![]() ,
,
(3)①当![]() 时,F点在三角形内部或边上,正方形PEFG在△BDC内部,
时,F点在三角形内部或边上,正方形PEFG在△BDC内部,
此时重叠部分图形的面积为正方形面积:![]() ,
,
②当![]() 时,如图:E点在三角形内部,F点在外部,
时,如图:E点在三角形内部,F点在外部,
∵GC=10-3t,NG=![]() CG=
CG=![]() (10-3t),FN=t-
(10-3t),FN=t-![]() (10-3t),FM=
(10-3t),FM=![]() ,
,

此时重叠部分图形的面积S=S正方形-S△FMN
![]() ,
,
③当![]() 时,重叠部分面积为梯形MPGN面积,如图:
时,重叠部分面积为梯形MPGN面积,如图:
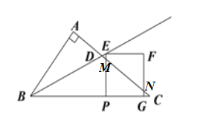
∵GC=10-3t,NG=![]() CG=
CG=![]() (10-3t),PC=10-2t,PM=
(10-3t),PC=10-2t,PM=![]() ,
,
∴![]() ,
,
综上所述:当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() .
.

 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案