题目内容
【题目】如图，将边长为3的正三角形ABC放置在直线l上（AB与直线l重合），将正三角形ABC沿直线l向右做无滑动的滚动，正三角形ABC的任意一边与直线l重合时记录滚动次数，例如，正三角形ABC由图中位置①滚动到位置②时记录为滚动一次，当正三角形ABC由图中位置①开始滚动2018次时，点A经过的路径总长度为（ ）
A.2690πB.2692πC.4034πD.4036π
【答案】B
【解析】
由题意知正三角形ABC每转动3次为一周期，且每个周期中点A转动的路径长度为
×2=4π，根据2018÷3=672…2知点A经过的路径总长度为672×4π+4π．
解：如图所示，
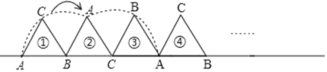
由题意知，正三角形ABC每转动3次为一周期，
在每个周期中点A转动的路径长度为
×2＝4π，
∵2018÷3＝672…2，
∴正三角形ABC由图中位置①开始滚动2018次时，点A经过的路径总长度为672×4π+4π＝2692π，
故选：B．
练习册系列答案
相关题目
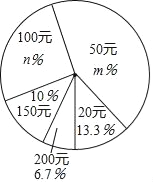
【题目】某中学在一次爱心捐款活动中，全体同学积极踊跃捐款．现抽查了九年级（1）班全班同学捐款情况，并绘制出如下的统计表和统计图：
捐款（元） | 20 | 50 | 100 | 150 | 200 |
人数（人） | 4 | 12 | 9 | 3 | 2 |
求：（Ⅰ）m=_____，n=_____；
（Ⅱ）求学生捐款数目的众数、中位数和平均数；
（Ⅲ）若该校有学生2500人，估计该校学生共捐款多少元？
