题目内容
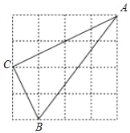
【题目】已知![]() ,在平面直角坐标系中,点A的坐标为(0,a),点B,点C的坐标分别为(-b,0),(b,0).
,在平面直角坐标系中,点A的坐标为(0,a),点B,点C的坐标分别为(-b,0),(b,0).
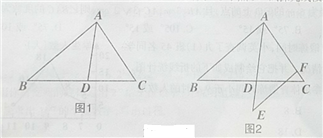
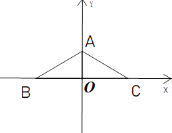
(1)如图,求点A,B,C的坐标;
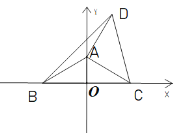
(2)如图,若点D在第一象限且满足AD=AC,∠DAC=90°,求BD;
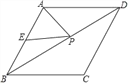
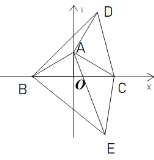
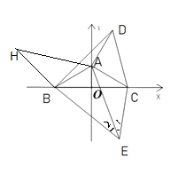
(3)如图,在(2)的条件下,若在第四象限有一点E,满足∠BEC=∠BDC,请探究BE,CE,AE之间的数量关系.
【答案】(1)A(0,1),B(![]() ,0),C(
,0),C(![]() ,0);(2)BD=
,0);(2)BD=![]() ;(3)BE+CE=
;(3)BE+CE=![]() AE
AE
【解析】
(1)根据二次根式有意义的条件和绝对值的非负性即可求解;
(2)在平面直角坐标系中,利用已知条件![]() ,
,![]() 构造全等直角三角形,再利用等腰直角三角形的性质求出
构造全等直角三角形,再利用等腰直角三角形的性质求出![]() 的长.
的长.
(3)要证明![]() 之间的数量关系,通常需要转化到同一个三角形中,通过构造全等三角形,把相同的线段转化到同一个三角形中,再利用全等三角形的性质和特殊三角形边之间的关系即可求得
之间的数量关系,通常需要转化到同一个三角形中,通过构造全等三角形,把相同的线段转化到同一个三角形中,再利用全等三角形的性质和特殊三角形边之间的关系即可求得
解:(1)![]()
![]()
![]()
![]()
![]()
(2)过点D作DH⊥y轴于点H,

过D作DG⊥x轴于G,则DG=HO=![]() ,
,![]() ,
,
![]() ,
,
![]()

(3)由(2)知,
∴∠BFC=60°
延长EB至H,使得BH=CE,连接AH
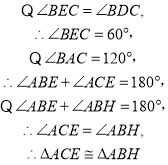

即![]() .
.

练习册系列答案
相关题目