题目内容
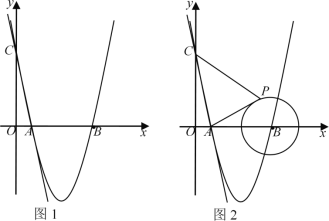
【题目】如图,顶点为M的抛物线y=ax2+bx+3与x轴交于A(3,0),B(﹣1,0)两点,与y轴交于点C.
(1)求抛物线的表达式;
(2)在直线AC的上方的抛物线上,有一点P(不与点M重合),使△ACP的面积等于△ACM的面积,请求出点P的坐标;
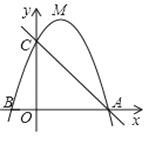
【答案】(1)![]() ;(2)P(2,3).
;(2)P(2,3).
【解析】
(1)抛物线的表达式为![]() ,即可求解;
,即可求解;
(2)过点M做直线m∥AC,直线m与抛物线的交点即为点P.
解:(1)∵y=ax2+bx+3与x轴交于A(3,0),B(﹣1,0)两点,
设抛物线解析式为:![]()
∴![]() 解得
解得![]()
∴抛物线的表达式为:![]()
(2)由(1)得抛物线的表达式为:![]()
∴顶点M的坐标为(1,4),点C坐标为(0,3)
设直线AC的解析式为:![]() ,把A(3,0)和C(0,3)代入得
,把A(3,0)和C(0,3)代入得
![]() 解得
解得![]()
∴直线AC的解析式为:![]()
过点M做直线m∥AC,直线m与抛物线的交点即为点P,
等底同高使△ACP的面积等于△ACM的面积.
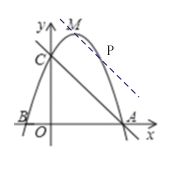
设直线m的表达式为:![]() ,
,
将M(1,4)代入得:b=5
∴直线m的表达式为:![]()
∴联立方程组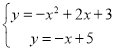 解得
解得![]()
![]()
∵点P不与点M重合
∴![]() 舍去
舍去
∴点P坐标为(2,3).
故答案为:(1)![]() ;(2)P(2,3).
;(2)P(2,3).

练习册系列答案
相关题目