Question

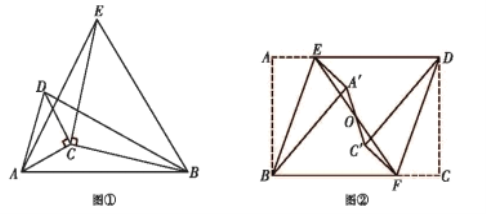
【题目】如图，四边形中，连接、，点为上一点，连接，为等边三角形，，，，，则_________．

Answer 1

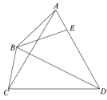
【答案】

【解析】

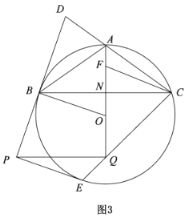
延长DA至F，使CD：EF=4:5，连接BF，过点F作FG⊥DB，交DB的延长线于G,过点B作BH⊥AD于H，即可证出△BCD∽△BEF，然后列出比例式求出BF，再利用锐角三角函数求出FG、BG和DG，再证出△BDH∽△FDG，求出BH、HD和AH，再利用勾股定理即可求出结论．

解：延长DA至F，使CD：EF=4:5，连接BF，过点F作FG⊥DB，交DB的延长线于G,过点B作BH⊥AD于H，

∵，

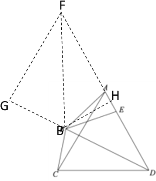
∴CD：EF=，∠BED＋∠BCD=180°

∴△BCD∽△BEF，∠EBC＋∠EDC=360°－（∠BED＋∠BCD）=180°

∴BD：BF=CD：EF=，∠CBD=∠EBF

∴8：BF=，∠CBE=∠DBF

解得BF=10

∵△ACD为等边三角形

∴CD=AD，∠EDC=60°

∴∠EBC=120°

∴∠DBF=120°

∴∠FBG=180°－∠DBF=60°

∴FG=BF·sin∠FBG=，BG= BF·cos∠FBG=5

∴DG=BD＋BG=13

根据勾股定理DF==

∵

∴CD=AD=4AE

∴EF=5AE

∴AF=EF－AE=4AE=AD

∴AF=AD=

∵∠BDH=∠FDG，∠BHD=∠FGD=90°

∴△BDH∽△FDG

∴

即

解得：DH=，BH=

∴AH=AD－DH=

在Rt△ABH中，AB=

故答案为：．