题目内容
【题目】作图题:要求尺规作图,不写作法,保留作图痕迹,写出结论。
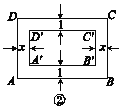
(1)如图所示,104国道OA和327国道OB在曲阜市相交于O点,在∠AOB的内部有工厂C和D,现要建一个货站P,使P到OA和OB的距离相等,且使PC=PD,用尺规作出P点的位置;
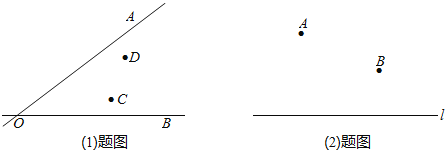
(2)在图中直线上找到一点M,使它到A、B两点的距离和最小。
【答案】(1)见解析;(2)见解析
【解析】
(1)分别作出∠AOB的角平分线及线段CD的垂直平分线,两条直线的交点即为所求P点;
(2)先作出点A关于直线l的对称点A′,连接A′B交直线l于点M,则点M即为所求.
解:(1)以O为圆心,以任意长为半径画圆,分别交OA,OB于E、F两点,再分别以E、F为圆心,以大于![]() EF为半径画圆,两圆相交于G点,连接OG;
EF为半径画圆,两圆相交于G点,连接OG;
连接CD,分别以C、D为圆心,以大于![]() CD为半径画圆,两圆相交于H、I两点,连接HI,直线HI于射线OG相交于P点,
CD为半径画圆,两圆相交于H、I两点,连接HI,直线HI于射线OG相交于P点,
则点P即为所求;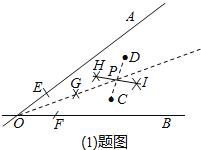
(2)如图,作出点A关于直线l的对称点A′,连接A′B交直线l于点M,则点M即为所求;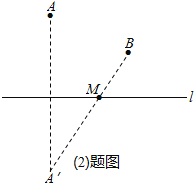 .
.

练习册系列答案
相关题目