题目内容
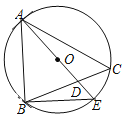
【题目】如图，在△ABC中，∠C=50°，圆O是△ABC的外接圆，AE为圆O的直径，AE与BC相交于点D，若AB=AD．则∠EAC=_______．
【答案】20°
【解析】
连接CE，由直径所对的圆周角是直角结合∠ACB=50°可求得∠BCE=40°，根据圆周角定理可得∠BAE=40°，由AB=AD可求出∠ADB=70°，最后由三角形外角的性质可求出结果．
连接CE，如图，
∵AE是⊙O的直径，
∴∠ACE=90°，
∵∠ACB=50°，
∴∠BCE=40°，
∵∠BAE，∠BCE是弧BE对的圆周角，
∴∠BAE=∠BCE=40°，
∵AB=AD，
∴∠ADB=
，
∵∠ADB=∠DAC+∠ACD，
∴∠DAC=∠ADB-∠ACB=70°-50°=20°．
即∠EAC=20°．
故答案为：20°．
练习册系列答案
相关题目
