题目内容
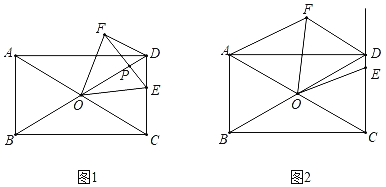
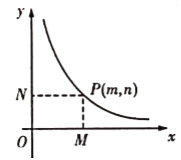
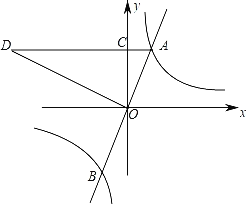
【题目】如图,直线y1=2x与双曲线y2=![]() 交于点A,点B,过点A作AC⊥y轴于点C,OC=2,延长AC至D,使CD=4AC,连接OD.
交于点A,点B,过点A作AC⊥y轴于点C,OC=2,延长AC至D,使CD=4AC,连接OD.
(1)求k的值;
(2)求∠AOD的大小;
(3)直接写出当y1>y2时,x的取值范围.
【答案】(1)2;(2)∠AOD=90°;(3)﹣1<x<0或x>1.
【解析】
(1)先求出A点坐标,然后代入y2=![]() ,即可确定k的值;
,即可确定k的值;
(2)先求出AC=1,CD=4,AD=5,由勾股定理求得OA2=OC2+AC2=22+12=5,OD2=OC2+CD2=22+42=20,再勾股定理的逆定理得到△AOD是直角三角形,即可证得∠AOD=90°;
(3)先求出点B的坐标,然后根据图象解答即可.
解:(1)∵OC=2,
∴C(0,2),
∵AC⊥y轴,
∴A的纵坐标为2,
将y=2代入y1=2x得,x=1,
∴A(1,2),
将A(1,2)代入y2=![]() 得,2=
得,2=![]() ,
,
∴k=2;
(2)∵A(1,2),
∴AC=1,
∴CD=4AC=4,
∴AD=5,
∵OC⊥AD,
∴OA2=OC2+AC2=22+12=5,OD2=OC2+CD2=22+42=20,
∴OA2+OD2=AD2=25,
∴△AOD是直角三角形,
∴∠AOD=90°;
(3)∵A(1,2),
∴B(﹣1,﹣2),
∴当y1>y2时,x的取值范围为﹣1<x<0或x>1.

 智能训练练测考系列答案
智能训练练测考系列答案【题目】某体育用品商店销售A,B两种型号的运动鞋,这两种运动鞋的进价与售价如下表,2018年第一季度的总利润为50 000元,其各月份的月利润占季度总利润的百分比如下图.
两种运动鞋的进价与售价表
A型号运动鞋 | B型号运动鞋 | |
进价(元/双) | 200 | 220 |
售价(元/双) | 250 | 280 |

(1)1月份的销售利润为 元;2月份的销售利润为 元,3月份的销售利润为_________元.
(2)如果A型运动鞋的2月份销量比1月份提高了20%,B型运动鞋的2月份销量是1月份的1.5倍,求1月份A、B两种运动鞋的销售量.
(3)已知3月份A型运动鞋的销售量超过B型运动鞋的销售量,问最多可能卖出B型运动鞋多少双.