题目内容
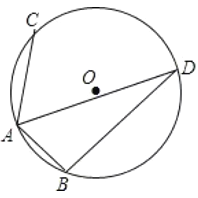
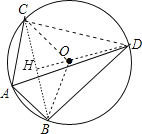
【题目】如图,⊙O的半径为4,A、B、C均是⊙O的点,点D是∠BAC的平分线与⊙O的交点,若∠BAC=120°,则弦BD的长为 _____________ .
【答案】4![]()
【解析】
连结BC、OB、OC,延长DO交BC与H,利用角平分线定义得∠BAD=∠CAD=![]() ∠BAC=60°,则根据圆周角定理得到∠DBC=∠BCD=60°,于是可判断△BCD为等边三角形,所以BD=BC,∠BDC=60°;再利用∠ABD=∠CAD得到弧DC=弧DB,根据垂径定理的推论得到DH⊥BC,BH=CH,接着根据圆周角定理计算出∠BOH=60°,然后在Rt△BOH中根据含30度的直角三角形三边的关系可计算出BH=2
∠BAC=60°,则根据圆周角定理得到∠DBC=∠BCD=60°,于是可判断△BCD为等边三角形,所以BD=BC,∠BDC=60°;再利用∠ABD=∠CAD得到弧DC=弧DB,根据垂径定理的推论得到DH⊥BC,BH=CH,接着根据圆周角定理计算出∠BOH=60°,然后在Rt△BOH中根据含30度的直角三角形三边的关系可计算出BH=2![]() ,则BC=2BH=4
,则BC=2BH=4![]() ,即BD=
,即BD=![]() .
.
解:连结BC、OB、OC,延长DO交BC与H,如图,
∵AD平分∠BAC,
∴∠BAD=∠CAD=![]() ∠BAC=60°,
∠BAC=60°,
∴∠DBC=∠BCD=60°,
∴△BCD为等边三角形,
∴BD=BC,∠BDC=60°,
∵∠ABD=∠CAD,
∴弧DC=弧DB,
∴DH⊥BC,
∴BH=CH,∠BOH=![]() ∠BOC,
∠BOC,
而∠BOC=2∠BDC=120°,
∴∠BOH=60°,
在Rt△BOH中,∵∠OBH=30°,
∴OH=![]() OB=2,
OB=2,
∴BH=![]() OH=
OH=![]() ,
,
∴BC=2BH=![]() ,
,
∴BD=![]() .
.
故答案为:![]() .
.

练习册系列答案
相关题目