Question

【题目】如图（1），在中，，，点分别是的中点，过点作直线的垂线段垂足为．点是直线上一动点，作使，连接．

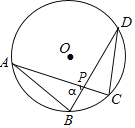
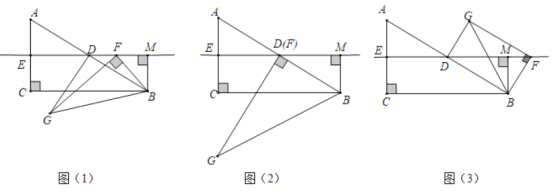
（1）观察猜想：如图（2），当点与点重合时，则的值为 ．

（2）问题探究：如图（1），当点与点不重合时，请求出的值及两直线夹角锐角的度数，并说明理由

（3）问题解决：如图（3），当点在同一直线上时，请直接写出的值．

Answer 1

【答案】（1）2；（2）60°，见解析；（3）4+或4－

【解析】

（1）由题意可知结论为当点F与点D重合时，则的值为2，并根据题意设BM=a，求出DM，GD即可解决问题；

（2）由题意可知结论为的值为2，两直线GD、ED夹角锐角的度数为60°，并利用全等三角形的判定定理证明△BGD∽△BFM，可得结论；

（3）根据题意分两种情形：当点G在线段AF上时以及当点G在线段AF的延长线上时，分别进行求解即可．

解：（1） 设BM=a．

∵AE=EC，AD=DB，

∴DE∥BC，

∴∠BDM=∠ABC=30°，

∵BM⊥EM，

∴∠BMD=90°，

∴，

在Rt△GDB中，∵∠GDB=90°，∠G=30°，

∴，

∴．

故答案为：2.

（2）在Rt△BDM中，设BM=a，则BD=2a，DM=a

在Rt△BGF中，设BF=b，则BG=2b，FG=

在△BGD与△BFM中，

∵BG：BF=2b：b=2a：a=BF：BM，∠DBG=60°－∠FBD=∠FBM

∴△BGD∽△BFM

则DG：FM=BD：BM=2a：a=2：1

即的值为2.

如图，延长GD、BF交于点P，

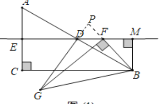
∵△BGD∽△BFM

∴∠PFD=∠MFB=∠BGD

则在△PDF与△PBG中，∠PDF=∠PBG=60°.

故的值为2，两直线GD、ED夹角锐角的度数为60°.

（3）如图，有以下两种如图3①，图3②

如图3③，ED是△ABC的中垂线；

∵在Rt△AF1B和Rt△AF2B中，DA=DF1=DF2=DB

∴四边形AF2BF1是矩形

当点G在线段AF上时，在Rt△BF1G1中，

设BF1=x，则BG1=2x=AG1，F1G1=

∴BG1：AF1=：=4－

当点G在线段AF的延长线上时，在矩形AF2BF1中，

设AF2=BF1=x， F2B=AF1=

∴BG2=2

则BG2：AF2=2：x=4+.

∴的值为4+或4－.