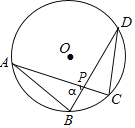
题目内容
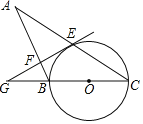
【题目】如图，⊙O的半径为5cm，弦AB＝
cm，CD＝
cm，则弦AC、BD的夹角∠APB的度数为_____．
【答案】105°
【解析】
首先连接OA、OB、OC，根据已知条件可以得出
为等腰直角三角形，从而得出∠ACB的度数，再过C点做直径CE，连接DE，进一步求出∠E的度数，从而得∠PBC的度数，故进一步得出∠APB的度数．
解：连接OA、OB、BC，作直径CE，连接DE，如图，
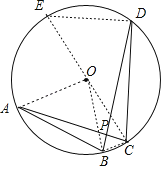
∵OA＝OB＝5，AB＝
，
∴OA2+OB2＝AB2，
∴为等腰直角三角形，
∴∠AOB＝90°，
∴∠ACB＝
∠AOB＝45°，
∵CE为直径，
∴∠CDE＝90°，
∵
＝
＝
＝
，
∴∠E＝60°，
∴∠PBC＝∠E＝60°，
∴∠APB＝45°+60°＝105°，
故答案为：105°．
练习册系列答案
相关题目
