题目内容
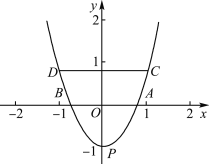
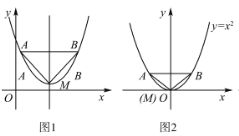
【题目】如图1,抛物线的顶点为M,平行于x轴的直线与该抛物线交于点A,B(点A在点B左侧),根据对称性△AMB恒为等腰三角形,我们规定:当△AMB为直角三角形时,就称△AMB为该抛物线的“完美三角形”.如图2,则抛物线y=x![]() 的“完美三角形”斜边AB的长________.
的“完美三角形”斜边AB的长________.
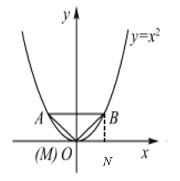
【答案】2.
【解析】
过点B做BN⊥x轴于N,得到△BON是等腰直角三角形,设点B坐标为(n,n),根据点B在抛物线y=x![]() 上,求出点B坐标为(1,1),点A坐标为(-1,1),问题得解.
上,求出点B坐标为(1,1),点A坐标为(-1,1),问题得解.
解:过点B做BN⊥x轴于N,
由题意得△AOB为等腰直角三角形,
∴∠ABO=45°,
∵AB∥x轴,
∴∠BON=45°
∴△BON是等腰直角三角形,
设点B坐标为(n,n),
∵点B在抛物线y=x![]() 上,
上,
∴n![]() =n
=n
解得n=1,或n=0(不合题意,舍去),
∴点B坐标为(1,1),
∴点A坐标为(-1,1),
∴AB=2.
故答案为:2

练习册系列答案
 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案
相关题目