题目内容
【题目】如图，四边形
中，AD∥BC，点
、
分别在
、
上，
，过点
、
分别作
的垂线，垂足为
、
．
(1)求证：△AGE≌△CHF；
(2)连接
，线段
与请交于点M，若CH=4，GH=10，求△AGM的面积．
【答案】（1）详见解析；（2）10.
【解析】
（1）由垂线的性质得出∠G=∠H=90°，AG∥CH，由平行线的性质和对顶角相等得出∠AEG=∠CFH，由AAS即可得出△AGE≌△CHF；
（2）连接AH、CG，证出四边形AHCG是平行四边形，得M为GH的中点，得出S△AGM=
S△AGH，即可得出结论．
(1)证明：
，
，
，
，
，
，
，
，
，
在
和
中，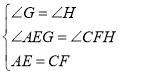
，
；
(2)连接AH、CG，如图所示：
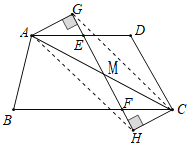
由（1）得：△AGE≌△CHF，
∴AG=CH，
∵AG∥CH，
∴四边形AHCG是平行四边形，
∴线段GH与AC互相平分．
∴点M为GH的中点，
∴S△AGM=S△AGH，
∵S△AGH=
，
∴△AGM的面积为10.
练习册系列答案
阅读快车系列答案
相关题目
