题目内容
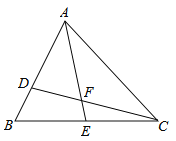
【题目】如图,在等腰直角△ACB中,∠ACB=90°,O是斜边AB的中点,点D、E分别在直角边AC、BC上,且∠DOE=90°,DE交OC于点P.有下列结论:
①∠DEO=45°;
②△AOD≌△COE;
③S四边形CDOE=![]() S△ABC;
S△ABC;
④![]() .
.
其中正确的结论序号为 .(把你认为正确的都写上)

【答案】①②③④.
【解析】
试题∵在等腰直角△ACB中,∠ACB=90°,O是斜边AB的中点,
∴∠A=∠B=∠ACO=°,OA=OC=OB,∠AOC=90°=∠DOE,
∴∠AOD=∠COE=90°-∠DOC,
在△AOD与△COE中,
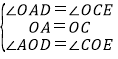 ,
,
∴△AOD≌△COE(ASA),
∴OD=OE,
∵∠EOD=90°,
∴∠DEO=45°,
∵△AOD≌△COE,∴S△AOD=S△COE,
∴S四边形CDOE=S△COD+S△COE=S△COD+S△AOD=S△AOC=![]() S△ABC,
S△ABC,
∵△DOE为等腰直角三角形,
∴∠DEO=45°.
∵∠DEO=∠OCE=45°,∠COE=∠COE,
∴△OEP∽△OCE,
∴![]() ,即OPOC=OE2,
,即OPOC=OE2,
即①②③④都正确;
故答案为:①②③④.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目