题目内容
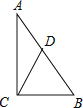
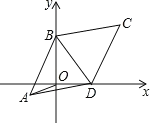
【题目】如图，已知平行四边形ABCD中，AB=BC，BC=10，∠BCD=60°，两顶点B、D分别在平面直角坐标系的y轴、x轴的正半轴上滑动，连接OA，则OA的长的最小值是_____．
【答案】
．
【解析】
利用邻边相等的平行四边形即菱形的性质以及等边三角形的性质确定A点位置，进而求出AO的长．
解：如图所示：过点A作AE⊥BD于点E，
当点A，O，E在一条直线上，此时AO最短．
∵平行四边形ABCD中，AB=BC，BC=10，∠BCD=60°，
∴AB=AD=CD=BC=10，∠BAD=∠BCD=60°，
∴△ABD是等边三角形，
∴AE过点O，E为BD中点，则此时
，
故AO的最小值为：AO=AE﹣EO=ABsin60°﹣
×BD=．
故答案为：．
练习册系列答案
相关题目
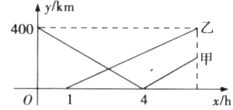
【题目】某单位要将一份宣传资料进行批量印刷．在甲印刷厂，在收取100元制版费的基础上，每份收费0.5元；在乙印刷厂，在收取40元侧版费的基础上，每份收费0.7元．设该单位要印刷此宣传资料
份（为正整数）．
（Ⅰ）根据题意，填写下表：
印剧数量（份） | 150 | 250 | 350 | 450 | … |
甲印刷厂收费（元） | 175 | ① | 275 | ② | … |
乙印刷厂收费（元） | 145 | 215 | ③ | 355 | … |
（Ⅱ）设在甲印刷厂收费
元，在乙印刷厂收费
元，分别写出，关于的函数解析式；
（Ⅲ）当
时，在哪家印刷厂花费少？请说明理由．
