Question

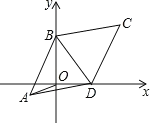
【题目】如图，在由边长为 1 个单位长度的小正方形组成的网格中，建立平面直角坐标系 A(1，7)， B(6，3)， C(2，3) ．

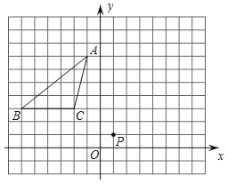
（1）将ABC 绕格点 P(1，1) 顺时针旋转90，得到△ ABC， 画出△ ABC，并写出下列各点坐标： A( ， 　 )， B( 　 　， )， C( ， )；

（2）找格点 M ，连CM ，使CM AB ，则点 M 的坐标为( )；

（3）找格点 N ，连 BN ，使 BN AC ，则点 N 的坐标为( )．

Answer 1

【答案】（1）图见解析，7,3；3,8；3,4；（2）图见解析，-6,8；（3）图见解析，-2,2

【解析】

（1）根据题意，将ABC 绕格点 P(1，1) 顺时针旋转90，即可得到△ ABC，然后根据平面直角坐标系即可求出结论；

（2）先求出tan∠ABC，然后在点B的正上方找出点M，使tan∠BMC=tan∠ABC，即可得出此时CM AB，即可得出结论；

（3）如解图所示，先求出tan∠CAE，然后找出点N，使tan∠NBC=tan∠CAE，即可证出BN AC ，从而求出结论．

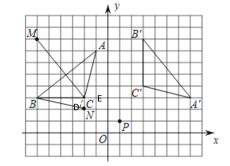
解：（1）将ABC 绕格点 P(1，1) 顺时针旋转90，即可得到△ABC，如下图所示，△ABC即为所求，由平面直角坐标系可知：A（7,3），B（），C（）

故答案为：7,3；；

（2）由图可知：tan∠ABC=

如图所示，在点B正上方找到点M（-6,8），连接CM、BM

由图可知：tan∠BMC=

∴tan∠BMC= tan∠ABC

∴∠BMC=∠ABC

∵∠ABC＋∠MBA=90°

∴∠BMC＋∠MBA=90°

∴CM⊥AB

∴点M（-6,8）即为所求

故答案为：-6,8．

（3）由图可知：tan∠CAE=

如图所示，找到点N（-2,2），连接BN，延长AC交BN于点D

由图可知：tan∠CBN=

∴tan∠CBN= tan∠CAE

∴∠CBN= ∠CAE

在Rt△ABE中，∠ABE＋∠BAC＋∠CAE=90°

∴∠ABE＋∠BAC ＋∠CBN =90°

∴∠ADB=90°，即BN AC ，

∴点N（-2,2）即为所求

故答案为：-2,2．