Question

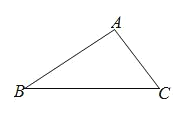
【题目】如图，在Rt△ABC中，∠ACB=90°，CD是斜边AB上的中线，那么下列结论错误的是（ ）

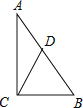
A.∠A+∠DCB=90°B.∠ADC= 2∠BC. AB=2CDD. BC=CD

Answer 1

【答案】D

【解析】

根据直角三角形斜边上的中线性质得出CD=AD=BD，根据等边对等角得出∠DCB=∠B，再逐个判断即可．

A、∵在Rt△ABC中，∠ACB=90°，CD是斜边AB上的中线，
∴CD=AD=BD=AB，
∴∠DCB=∠B，
∵∠ACB=90°，
∴∠A+∠B=90°，
∴∠A+∠DCB=90°，故本选项正确，不合题意；
B、∵∠DCB=∠B，∠ADC=∠B+∠DCB，
∴∠ADC=2∠B，故本选项正确，不合题意；
C、∵在Rt△ABC中，∠ACB=90°，CD是斜边AB上的中线，
∴AB=2CD，故本选项正确，不合题意；
D、根据已知不能推出BC=CD，故本选项错误，符合题意；
故选：D．