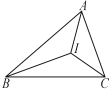
题目内容
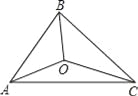
【题目】如图![]() ,
,![]() 平分
平分![]() ,点
,点![]() 、
、![]() 、
、![]() 分别是射线
分别是射线![]() 、
、![]() 、
、![]() 上的点(点
上的点(点![]() 、
、![]() 、
、![]() 不与点
不与点![]() 重合),联结
重合),联结![]() ,交射线
,交射线![]() 与点
与点![]() .
.
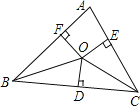
(1)如果![]() ,
,![]() 平分
平分![]() ,试判断
,试判断![]() 与射线
与射线![]() 的位置关系,试说明理由;
的位置关系,试说明理由;
(2)如果![]() ,
,![]() ,垂足为点
,垂足为点![]() ,
,![]() 中有两个相等的角,请直接写出
中有两个相等的角,请直接写出![]() 的大小.
的大小.
【答案】(1)![]() 与射线
与射线![]() 垂直,理由见解析;(2)
垂直,理由见解析;(2)![]() 的大小为
的大小为![]() 或
或![]() 或
或![]() .
.
【解析】
(1)先根据平行线的性质、角平分线的定义得出![]() ,再根据角平分线的定义得出
,再根据角平分线的定义得出![]() ,最后根据三角形的外角性质、领补角的定义即可得出结论;
,最后根据三角形的外角性质、领补角的定义即可得出结论;
(2)先根据角平分线的定义、直角三角形的性质求出![]() 和
和![]() 的度数,再根据“
的度数,再根据“![]() 中有两个相等的角”分三种情况,然后分别根据三角形的外角性质、角的和差求解即可得.
中有两个相等的角”分三种情况,然后分别根据三角形的外角性质、角的和差求解即可得.
(1)![]() 与射线
与射线![]() 垂直,理由如下:
垂直,理由如下:
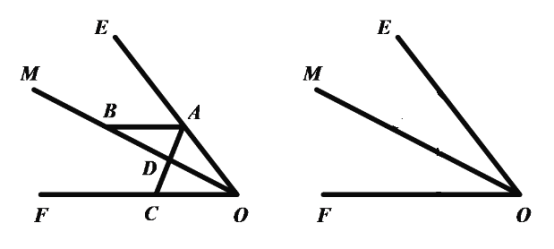
如图1,![]()
![]()
![]() 平分
平分![]() ,
,![]() 平分
平分![]()
![]() ,
,![]()
![]()
由三角形的外角性质得:![]()
![]()
又![]()
![]()
![]()
即![]() 与射线
与射线![]() 垂直;
垂直;
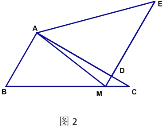
(2)![]() 平分
平分![]() ,
,![]()
![]()
![]()
![]()
![]()
如图2,由题意,分以下三种情况:
①当![]() 时
时
![]() (三角形的外角性质)
(三角形的外角性质)
②当![]() 时
时
![]()
③当![]() 时
时
![]()
则![]()
解得![]()
综上,![]() 的大小为
的大小为![]() 或
或![]() 或
或![]() .
.

练习册系列答案
相关题目