题目内容
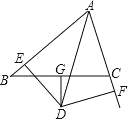
【题目】如图，G 为 BC 的中点，且 DG⊥BC，DE⊥AB 于 E，DF⊥AC 于 F， BE＝CF．
（1）求证：AD 是∠BAC 的平分线；
（2）如果 AB＝8，AC＝6，求 AE 的长．
【答案】（1）见解析；（2）7.
【解析】
（1）因为G为BC的中点，且DG⊥BC，则DG是线段BC的垂直平分线，考虑连接DB、DC，利用线段的垂直平分线的性质，又因为DE⊥AB，DF⊥AC，可通过DE=DF说明AD是∠BAC的平分线；
（2）先通过△AED与△ADF的全等关系，说明AE与AF的关系，利用线段的和差关系，通过线段的加减求出AE的长．
（1）连接BD、DC
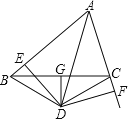
∵DG⊥BC，G为BC的中点，
∴BD=CD，
∵DG⊥BC，DE⊥AB
∴∠BED=∠CFD，
在Rt△DBE和Rt△DFC中，
∴△DBE≌△DFC
∴DE=DF，
∴∠BAD=∠FAD
∴AD是∠BAC的平分线；
（2）∵DE=DF，∠BAD=∠FAD，AD=AD
∴△AED≌△ADF，
∴AE=AF
∵AB=AE+BE，AC=AF-CF，
∴AB+AC=AE+AF，
∵AB=8，AC=6，
∴8+6=2AE，
∴AE=7．
练习册系列答案
口算题天天练系列答案
相关题目
