题目内容
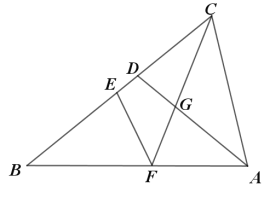
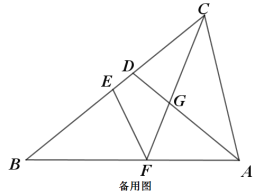
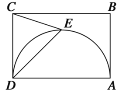
【题目】如图,在边长为4的正方形ABCD中,点E为对角线AC上一动点(点E与点A,C不重合),连接DE,作EF⊥DE交射线BA于点F,过点E作MN∥BC分别交CD,AB于点M、N,作射线DF交射线CA于点G.
(1)求证:EF=DE;
(2)当AF=2时,求GE的长.

【答案】(1)见解析;(2)![]()
【解析】
(1)根据正方形的性质以及EF⊥DE,证明△DME≌△ENF即可;
(2)根据勾股定理计算出DF,根据平行线的性质得到![]() ,计算出DG,FG的值,利用特殊角的锐角三角函数计算出DE的值,最后证明△DGE∽△AGF,利用相似比列出方程即可求出GE的值.
,计算出DG,FG的值,利用特殊角的锐角三角函数计算出DE的值,最后证明△DGE∽△AGF,利用相似比列出方程即可求出GE的值.
(1)证明:∵四边形ABCD是正方形,且MN∥BC,
∴四边形ANMD是矩形,∠BAC=45°,
∴∠ANM=∠DMN=90°,EN=AN=DM,
∴∠DEM+∠EDM=90°,
∵EF⊥DE,
∴∠DEM+∠FEN=90°,
∴∠EDM=∠FEN,
∴在△DME与△ENF中
∠DME=∠ENF=90°,DM=EN,∠EDM=∠FEN,
∴△DME≌△ENF(ASA),
∴EF=DE;
(2)∵四边形ABCD是正方形,
∴AB∥DC,∠DAB=90°,
∴DF=![]() ,
,
∴![]() ,即
,即![]() ,解得:DG=
,解得:DG=![]() ,
,
∴FG=DF-DG=![]() ,
,
又∵DE=EF,EF⊥DE,
∴△DEF是等腰直角三角形,
∴∠EDF=45°,DE=EF=![]() ,
,
∴∠GAF=∠GDE=45°,
又∵∠DGE=∠AGF,
∴△DGE∽△AGF,
∴![]() ,即
,即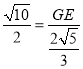 ,解得:
,解得:![]() ,
,
∴![]() .
.

练习册系列答案
相关题目