题目内容
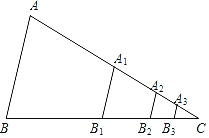
【题目】如图,在![]() 中
中![]()
![]() ,连接
,连接![]() ,点
,点![]() ,
,![]() 分别是
分别是![]() 的点(点
的点(点![]() 不与点
不与点![]() 重合),
重合),![]() ,
,![]() 相交于点
相交于点![]() .
.
(1)求![]() ,
,![]() 的长;
的长;
(2)求证:![]() ~
~![]() ;
;
(3)当![]() 时,请直接写出
时,请直接写出![]() 的长.
的长.
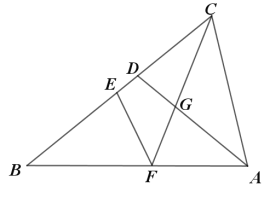
【答案】(1)AD=10,BD=10;(2)见解析;(3)AG=![]() .
.
【解析】
(1)由![]() 可证明△ABC∽△DAC,通过相似比即可求出AD,BD的长;
可证明△ABC∽△DAC,通过相似比即可求出AD,BD的长;
(2)由(1)可证明∠B=∠DAB,再根据已知条件证明∠AFC=∠BEF即可;
(3)过点C作CH∥AB,交AD的延长线于点H,根据平行线的性质得到![]() ,计算出CH和AH的值,由已知条件得到
,计算出CH和AH的值,由已知条件得到![]() ≌
≌![]() ,设AG=x,则AF=15-x,HG=18-x,再由平行线的性质得到
,设AG=x,则AF=15-x,HG=18-x,再由平行线的性质得到![]() ,表达出即可解出x,即AG的值.
,表达出即可解出x,即AG的值.
解:(1)∵![]() ,
,
∴![]() ,
,
又∵∠ACB=∠DCA,
∴△ABC∽△DAC,
∴![]() ,即
,即![]() ,
,
解得:CD=8,AD=10,
∴BD=BC-CD=18-8=10,
∴AD=10,BD=10;
(2)由(1)可知,AD=BD=10,
∴∠B=∠DAB,
∵∠AFE=∠B+∠BEF,
∴∠AFC+∠CFE=∠B+∠BEF,
∵![]() ,
,
∴∠AFC=∠BEF,
又∵∠B=∠DAB,
∴![]() ~
~![]() ;
;
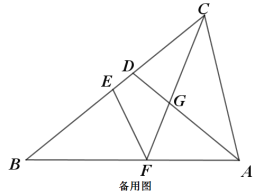
(3)如图,过点C作CH∥AB,交AD的延长线于点H,
∴![]() ,
,
即![]() ,解得:CH=12,HD=8,
,解得:CH=12,HD=8,
∴AH=AD+HD=18,
若![]() ,
,
则![]() ≌
≌![]() ;
;
∴BF=AG,
设AG=x,则AF=15-x,HG=18-x,
∵CH∥AB,
∴![]() ,即
,即![]() ,
,
解得:![]() ,
,![]() (舍去)
(舍去)
∴AG=![]() .
.

练习册系列答案
相关题目