Question

【题目】(1)如图1，将矩形折叠，使落在对角线上，折痕为，点落在点 处，若，则 ;

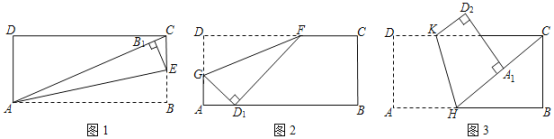
(2)小丽手中有一张矩形纸片，，.她准备按如下两种方式进行折叠:

①如图2，点在这张矩形纸片的边上，将纸片折叠，使点落在边上的点处，折痕为，若，求的长;

②如图3，点在这张矩形纸片的边上，将纸片折叠，使落在射线上，折痕为，点，分别落在，处，若，求的长.

Answer 1

【答案】（1）12；（2）①AG=;②

【解析】

（1）由折叠的性质可得∠BAE＝∠CAE＝12°；

（2）①过点F作FH⊥AB于H，可证四边形DFHA是矩形，可得AD＝FH＝4，由勾股定理可求D1H＝3，由勾股定理可求AG的长；

②首先证明CK＝CH，利用勾股定理求出BH，可得AH，再利用翻折不变性，可知AH＝A1H，由此即可解决问题.

解：（1）∵∠DAC＝66°，

∴∠CAB＝24°

∵将矩形ABCD折叠，使AB落在对角线AC上，

∴∠BAE＝∠CAE＝12°

故答案为：12；

（2）如图2，过点F作FH⊥AB于H，

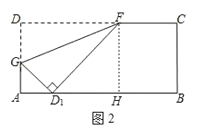
∵∠D＝∠A＝90°，FH⊥AB

∴四边形DFHA是矩形

∴AD＝FH＝4，

∵将纸片ABCD折叠

∴DF＝D1F＝5，DG＝D1G，

∴D1H＝，

∴AD1＝2

∵AG2＋D1A2＝D1G2，

∴AG2＋4＝（4AG）2，

∴AG＝；

②∵DK＝，CD＝9，

∴CK＝9＝，

∵四边形ABCD是矩形，

∴DC∥AB，

∴∠CKH＝∠AHK，

由翻折不变性可知，∠AHK＝∠CHK，

∴∠CKH＝∠CHK，

∴CK＝CH＝，

∵CB＝AD＝4，∠B＝90°，

∴在Rt△CDF中，BH＝，

∴AH＝ABBH＝，

由翻折不变性可知，AH＝A1H＝，

∴A1C＝CHA1H＝3．