题目内容
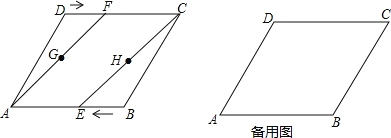
【题目】如图,在菱形![]() ,
,![]() ,
,![]() .动点
.动点![]() 、
、![]() 分别从点
分别从点![]() 、
、![]() 同时出发,以
同时出发,以![]() 的速度向点
的速度向点![]() 、
、![]() 运动,连接
运动,连接![]() 、
、![]() ,取
,取![]() 、
、![]() 的中点
的中点![]() 、
、![]() ,连接
,连接![]() 、
、![]() .设运动的时间为
.设运动的时间为![]() .
.
(1)求证:![]() ;
;
(2)当![]() 为何值时,四边形
为何值时,四边形![]() 为菱形;
为菱形;
(3)试探究:是否存在某个时刻![]() ,使四边形
,使四边形![]() 为矩形,若存在,求出
为矩形,若存在,求出![]() 的值,若不存在,请说明理由.
的值,若不存在,请说明理由.
【答案】(1)证明详见解析;(2)1;(3)不存在,理由详见解析
【解析】
(1)根据菱形的性质得到∠B=∠D,AD=BC,AB∥DC,推出△ADF≌△CBE,根据全等三角形的性质得到∠DFA=∠BEC,根据平行线的判定定理即可得到结论;
(2)过D作DM⊥AB于M,连接GH,EF,推出四边形AECF是平行四边形,根据菱形的判定定理即可得到四边形EGFH是菱形,证得四边形DMEF是矩形,于是得到ME=DF=t列方程即可得到结论;
(3)不存在,假设存在某个时刻t,使四边形EHFG为矩形,根据矩形的性质列方程即可得到结果.
解:(1)证明:∵动点E、F同时运动且速度相等,
∴DF=BE,
∵四边形ABCD是菱形,
∴∠B=∠D,AD=BC,AB∥DC,
在△ADF与△CBE中,
 ,
,
∴△ADF≌△CBE,
∴∠DFA=∠BEC,
∵AB∥DC,
∴∠DFA=∠FAB,
∴∠FAB=∠BEC,
∴AF∥CE;
(2)如图,过D作DM⊥AB于M,连接GH,EF,

∴DF=BE=t,
∵AF∥CE,AB∥CD,
∴四边形AECF是平行四边形,
∵G、H是AF、CE的中点,
∴GH∥AB,
∵四边形EGFH是菱形,
∴GH⊥EF,
∴EF⊥AB,∠FEM=90°,
∵DM⊥AB,
∴DM∥EF,
∴四边形DMEF是矩形,
∴ME=DF=t,
∵AD=4,∠DAB=60°,DM⊥AB,
∴![]() ,
,
∴BE=4-2-t=t,
∴t=1;
(3)不存在,假设存在某个时刻t,使四边形EHFG为矩形,
∵四边形EHFG为矩形,
∴EF=GH,
∴![]() ,
,
即![]() ,
,
解得t=0,0<t<4,
∴与原题设矛盾,
∴不存在某个时刻t,使四边形EHFG为矩形.

 备战中考寒假系列答案
备战中考寒假系列答案【题目】某体育用品商店购进了足球和排球共20个,一共花了1360元,进价和售价如表:
足球 | 排球 | |
进价(元/个) | 80 | 50 |
售价(元/个) | 95 | 60 |
(l)购进足球和排球各多少个?
(2)全部销售完后商店共获利润多少元?






