题目内容
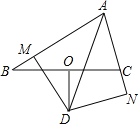
【题目】如图，△ABC中，O是BC的中点，D是∠BAC平分线上的一点，且DO⊥BC，过点D分别作DM⊥AB于M，DN⊥AC于N．求证：BM＝CN．
【答案】见解析．
【解析】
根据O是BC的中点，DO⊥BC，可知OD是BC的垂直平分线，那么BD＝CD，而AD是∠BAC的平分线，DM⊥AB，DN⊥AC，根据角平分线的性质可得DM＝DN，再根据HL可判定Rt△BMD≌Rt△CND，从而有BM＝CN．
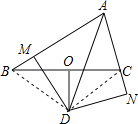
证明：连接BD，CD，如图，
∵O是BC的中点，DO⊥BC，
∴OD是BC的垂直平分线，
∴BD＝CD，
∵AD是∠BAC的平分线，DM⊥AB，DN⊥AC，
∴DM＝DN，
在Rt△BMD和Rt△CND中，
，
∴Rt△BMD≌Rt△CND，
∴BM＝CN．
练习册系列答案
名校课堂系列答案
相关题目
