Question

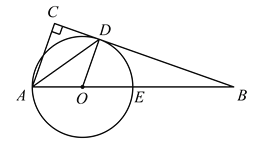
【题目】点A，B，C在⊙O上，∠ABO=31°，∠ACO=39°，则∠BOC的度数为______．

Answer 1

【答案】140°或16°

【解析】

过A、O作⊙O的直径AD，分别在等腰△OAB、等腰△OAC中，根据三角形外角的性质即可得出结论．

过A作⊙O的直径，交⊙O于D．

如下图，在△OAB中，∵OA=OB，∴∠OAB=∠OBA，∴∠BOD=∠OBA+∠OAB=2×31°=62°，同理可得：∠COD=∠OCA+∠OAC=2×39°=78°，∴∠BOC=∠BOD+∠COD=140°．

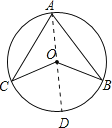
如下图，B,C在同侧时，由于∠A+∠C+∠ADC=∠O+∠B+∠ODB=180°

且∠ADC=∠ODB，所以∠O-∠A=∠C-∠B=8°

又因为∠O=2∠A

所以∠BOC=16°

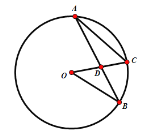
故答案为：140°或16°．