��Ŀ����
����Ŀ����ͼ������ABCD�У�AB=6cm��BC=8cm��E��F�ǶԽ���AC�ϵ��������㣬�ֱ��A��Cͬʱ������������У��ٶȾ�Ϊ2cm/s���˶�ʱ��Ϊt��0��t��5���룮
��1����G��H�ֱ���AB��DC���е㣬��t��2.5s����֤����E��G��F��HΪ������ı���ʼ����ƽ���ı��Σ�
��2���ڣ�1���������£���tΪ��ֵʱ����E��G��F��HΪ������ı����Ǿ��Σ�
��3����G��H�ֱ�������A-B-C��C-D-A�ϵĶ��㣬�ֱ��A��C��ʼ����E��F��ͬ���ٶ�ͬʱ��������tΪ��ֵʱ����E��G��F��HΪ������ı��������Σ���ֱ��д��t��ֵ��
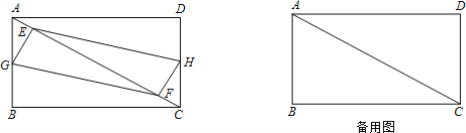
���𰸡���1��֤������������2����tΪ4.5���0.5��ʱ���ı���EGFH�Ǿ��Σ���3��tΪ![]() ��ʱ���ı���EGFH�����Σ�
��ʱ���ı���EGFH�����Σ�
��������
��1�����ݹ��ɶ������AC��֤����AFG�ա�CEH������ȫ�������ε����ʵõ�GF=HE�������ڴ�����ȵ�GF��HE������ƽ���ı��ε��ж��ɵý��ۣ�
��2����ͼ1������GH����AC-AE-CF=8��AE+CF-AC=8����������з��̼��㼴�ɣ�
��3������AG��CH���ж��ı���AGCH�����Σ��õ�AG=CG�����ݹ��ɶ������BG���õ�AB+BG�ij�������������
�⣺��1�����ı���ABCD�Ǿ��Σ�
��AB=CD��AB��CD��AD��BC����B=90����
���BAC=��DCA��
��AB=6cm��BC=8cm��
��AC=10cm��
��G��H�ֱ���AB��DC���е㣬
��AG=![]() AB��CH=
AB��CH=![]() CD��
CD��
��AG=CH��
��E��F�ǶԽ���AC�ϵ��������㣬�ֱ��A��Cͬʱ������������У��ٶȾ�Ϊ2cm/s��
��AE=CF��
��AF=CE��
���AGF�ա�CHE��SAS����
��GF=HE����AFG=��CEH��
��GF��HE��
����E��G��F��HΪ������ı���ʼ����ƽ���ı��Σ�
��2����ͼ1������GH���ɣ�1����֪�ı���EGFH��ƽ���ı��Σ�
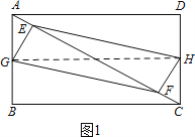
��G��H�ֱ���AB��DC���е㣬
��GH=BC=8cm��
�൱EF=GH=8cmʱ���ı���EGFH�Ǿ��Σ������������
����AE=CF=2t����EF=10-4t=8����ã�t=0.5��
����AE=CF=2t����EF=2t+2t-10=8����ã�t=4.5��
����tΪ4.5���0.5��ʱ���ı���EGFH�Ǿ��Σ�
��3����ͼ2������AG��CH��
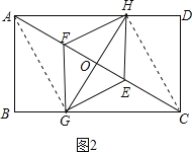
���ı���GEHF�����Σ�
��GH��EF��OG=OH��OE=OF��
��AF=CE
��OA=OC��
���ı���AGCH�����Σ�
��AG=CG��
��AG=CG=x����BG=8-x��
�ɹ��ɶ����ã�AB2+BG2=AG2��
��62+��8-x��2=x2����ã�x=![]() ��
��
��BG=8-![]() =
=![]() ��
��
��AB+BG=6+![]() =
=![]() ��
��
t=![]() ��2=
��2=![]() ��
��
��tΪ![]() ��ʱ���ı���EGFH�����Σ�
��ʱ���ı���EGFH�����Σ�