Question

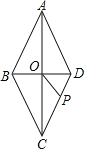
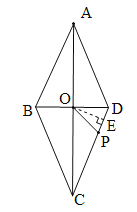
【题目】如图，在菱形ABCD中，两对角线AC、BD交于点O，AC=8，BD=6，当△OPD是以PD为底的等腰三角形时，CP的长为（　　）

A. 2B. C. D.

Answer 1

【答案】C

【解析】

过O作OE⊥CD于E．根据菱形的对角线互相垂直平分得出OB，OC的长，AC⊥BD，再利用勾股定理列式求出CD，然后根据三角形的面积公式求出OE．在Rt△OED中，利用勾股定理求出ED．根据等腰三角形三线合一的性质得出PE ，利用CP=CD-PD即可得出结论．

过O作OE⊥CD于E．

∵菱形ABCD的对角线AC、BD相交于点O，∴OBBD6=3，OA=OCAC8=4，AC⊥BD，由勾股定理得：CD5．

∵OC×OD=CD×OE，∴12=5OE，∴OE=2.4．在Rt△ODE中，DE===1.8．

∵OD=OP，∴PE=ED=1.8，∴CP=CD-PD=5-1.8-1.8=1.4=．

故选C．