题目内容
【题目】如图（1），在平面直角坐标系中，抛物线y=﹣ 
x2+bx+c与x轴交于点A（﹣4，0），与y轴交于点B（0，4）．
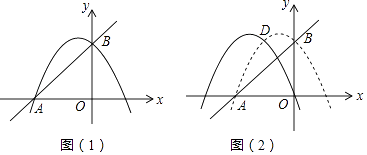
（1）求抛物线的函数解析式；
（2）在x轴上有一点P，点P在直线AB的垂线段为PC，C为垂足，且PC= 
，求点P的坐标；
（3）如图（2），将原抛物线向左平移，使平移后的抛物线过原点，与原抛物线交于点D，在平移后的抛物线上是否存在点E，使S△APE=S△ACD？若存在，请求出点E的坐标，若不存在，请说明理由．
【答案】
（1）
解：∵抛物线y=﹣ 
x2+bx+c过点A（﹣4，0），B（0，4），
∴ 
，解得： 
，
∴所求抛物线的函数解析式是y=﹣ x2﹣x+4
（2）
解：∵A（﹣4，0），B（0，4），
∴OA=OB=4．
∵∠AOB=90°，
∴∠OAB=∠OBA=45°．
设PC⊥AB，则∠ACP=90°，PC= 
．
Rt△ACP中，sin∠PAC= 
，
∴PA= 
=2．
∴OP=OA﹣PA=2或OP=OA+AP=6．
∴点P的坐标为：P1（﹣2，0），P2（﹣6，0）
（3）
解：∵抛物线y=﹣ x2﹣x+4向左平移后过原点，
∴平移后的抛物线的函数解析式为y=﹣ x2﹣3x．
由﹣ x2﹣x+4=﹣ x2﹣3x．
解得 x=﹣2．
∴y=﹣ ×（﹣2）2﹣3×（﹣2）=4．
∴点D的坐标为（﹣2，4）．
如图2，①当点P在AO上时，设P1C1⊥AB，过C1作C1N⊥x轴，垂足为N，
在Rt△AC1P1中，∵∠C1AP1=45°，AP1=2，
∴AC1=P1C1= ．
∴AN=NC1=1．
∴点C1的坐标为（﹣3，1）．
∴ 
= 
﹣ 
﹣ 
= ×2×4﹣ ×2×1﹣ ×4×1=4﹣1﹣2=1．
②当点P在OA延长线上时，同理可得点C2的坐标为（﹣5，﹣1）． 
=1，
设点E（a，b），当S△APE=S△ACD时，有 ×2×|b|=1．即|﹣ a2﹣3a|=1．
∴﹣ a2﹣3a=1或﹣ a2﹣3a=﹣1．
∴a1=﹣3+ 
，a2=﹣3﹣ ，a3=﹣3+ 
，a4=﹣3﹣ ．
∴存在点E，使S△APE=S△ACD，点E的坐标为：（﹣3+ ，1）或（﹣3﹣ ，﹣1）或（﹣3+ ，﹣1）或（﹣3﹣ ，﹣1）
【解析】（1）由A、B两点的坐标可求得解析式；（2）由OA=OB=4知∠OAB=∠OBA=45°，根据sin∠PAC= 、PC= 可得PA的长，从而由OP=OA﹣PA或OP=OA+AP得出答案；（3）由平移后的抛物线y=﹣ x2﹣3x得出D（﹣2，4），分点P在AO上和点P在OA延长线上利用割补法求得△ACD的面积为1，设点E（a，b），根据S△APE=S△ACD得 ×2×|b|=1．即|﹣ a2﹣3a|=1，解方程即可得出答案．
