题目内容
【题目】如图,AB为⊙O的直径,C为半圆上一动点,过点C作⊙O的切线l的垂线BD,垂足为D,BD与⊙O交于点E,连接OC,CE,AE,AE交OC于点F. 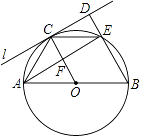
(1)求证:△CDE≌△EFC;
(2)若AB=4,连接AC. ①当AC=时,四边形OBEC为菱形;
②当AC=时,四边形EDCF为正方形.
【答案】
(1)证明:如图,

∵BD⊥CD,
∴∠CDE=90°,
∵AB是直径,
∴∠AEB=90°,
∵CD是切线,
∴∠FCD=90°,
∴四边形CFED矩形,
∴CF=DE,EF=CD,
在△CDE和△EFC中,
 ,
,
∴△CDE≌△EFC.
(2)2;2 ![]()
【解析】(2)解:①当AC=2时,四边形OCEB是菱形. 理由:连接OE.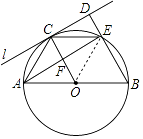
∵AC=OA=OC=2,
∴△ACO是等边三角形,
∴∠CAO=∠AOC=60°,
∵∠AFO=90°,
∴∠EAB=30°,
∵∠AEB=90°,
∴∠B=60°,∵OE=OB,
∴△OEB是等边三角形,
∴∠EOB=60°,
∴∠COE=180°﹣60°﹣60°=60°,∵CO=OE,
∴△COE是等边三角形,
∴CE=CO=OB=EB,
∴四边形OCEB是菱形.
所以答案是2.
②当四边形DEFC是正方形时,
∵CF=FE,
∵∠CEF=∠FCE=45°,
∵OC⊥AE,
∴ ![]() ,
,
∴∠CAE=∠CEA=45°,
∴∠ACE=90°,
∴AE是⊙O的直径,
∴ ![]() ,
,
∴△AOC是等腰直角三角形,
∴AC= ![]() OA=2
OA=2 ![]() .
.
∴AC=2 ![]() 时,四边形DEFC是正方形.
时,四边形DEFC是正方形.
所以答案是2 ![]() .
.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】为了对学生进行多元化的评价,某中学决定对学生进行综合素质评价![]() 设该校中学生综合素质评价成绩为x分,满分为100分评价等级与评价成绩x分之间的关系如下表:
设该校中学生综合素质评价成绩为x分,满分为100分评价等级与评价成绩x分之间的关系如下表:
中学生综合素质评价成绩 | 中学生综合素质评价等级 |
| A级 |
| B级 |
| C级 |
| D级 |
现随机抽取该校部分学生的综合素质评价成绩,整理绘制成图![]() 、图
、图![]() 两幅不完整的统计图
两幅不完整的统计图![]() 请根据相关信息,解答下列问题:
请根据相关信息,解答下列问题:
(1)在这次调查中,一共抽取了______名学生,图![]() 中等级为D级的扇形的圆心角
中等级为D级的扇形的圆心角![]() 等于______
等于______![]() ;
;
(2)补全图![]() 中的条形统计图;
中的条形统计图;
(3)若该校共有1200名学生,请你估计该校等级为C级的学生约有多少名.