题目内容
【题目】如图(1),四边形ABCD是平行四边形,BD是它的一条对角线,过顶点A、C分别作AM⊥BD,CN⊥BD,M,N为垂足. 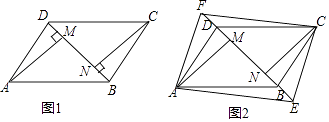
(1)求证:AM=CN;
(2)如图(2),在对角线DB的延长线及反向延长线上分别取点E,F,使BE=DF,连接AE、CF,试探究:当EF满足什么条件时,四边形AECF是矩形?并加以证明.
【答案】
(1)证明:∵四边形ABCD是平行四边形,
∴AD=BC,AD∥BC,∠ADM=∠CBN.
∵AM⊥BD,CN⊥BD,
∴∠AMD=∠CNB=90°,
在△AMD和△CNB中  ,
,
∴△AMD≌△CNB.
∴AM=CN.
(2)猜想:当EF=AC时,四边形AECF是矩形.
证明:由(1)得△AMD≌△CNB,
∴DM=BN.
∵BE=DF,
∴DM+DF=BN+BE,即MF=NE.
在△AMF和△CNE中 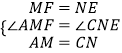
∴△AMF≌△CNE.
∴AF=CE,∠AFE=∠CEF.
∴AF∥CE且AF=CE.
即四边形AECF是平行四边形.
又EF=AC,
∴四边形AMCN是矩形
【解析】(1)利用平行四边形的性质证得△AMD≌△CNB,从而根据全等三角形对应边相等证得结论即可;(2)利用对角线相等的平行四边形是矩形证得结论即可.
【考点精析】通过灵活运用平行四边形的性质和矩形的判定方法,掌握平行四边形的对边相等且平行;平行四边形的对角相等,邻角互补;平行四边形的对角线互相平分;有一个角是直角的平行四边形叫做矩形;有三个角是直角的四边形是矩形;两条对角线相等的平行四边形是矩形即可以解答此题.

练习册系列答案
 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案
相关题目