题目内容
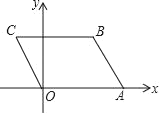
【题目】如图,已知A(4,0),B(3,3),以OA、AB为边作OABC,则若一个反比例函数的图象经过C点,则这个反比例函数的表达式为_____.
【答案】y=﹣![]() .
.
【解析】
过B作BE⊥x轴,过C作CD⊥x轴,可得∠BEA=∠CDO=90°,由四边形ABCO为平行四边形,得到对边平行且相等,利用两直线平行得到一对同位角相等,利用AAS得到三角形ABE与三角形OCD全等,利用全等三角形对应边相等得到AE=OD,BE=CD,确定出C的坐标,利用待定系数法确定出反比例函数的解析式,即可得出答案.
过B作BE⊥x轴,过C作CD⊥x轴,可得∠BEA=∠CDO=90°,
∵四边形ABCO为平行四边形,
∴AB∥OC,AB=OC,
∴∠BAE=∠COD,
在△ABE和△OCD中,

∴△ABE≌△OCD(AAS),
∴BE=CD,AE=OD,
∵A(4,0),B(3,3),
∴OA=4,BE=OE=3,
∴AE=OA﹣OE=4﹣3=1,
∴OD=AE=1,CD=BE=3,
∴C(﹣1,3),
设过点C的反比例解析式为y=![]() ,
,
把C(﹣1,3)代入得:k=﹣3,
则反比例解析式为y=﹣![]() .
.
故答案为:y=﹣![]()


练习册系列答案
 天天练口算系列答案
天天练口算系列答案
相关题目