题目内容
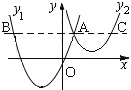
【题目】如图, 抛物线![]() 与
与![]() 交于点A
交于点A![]() ,过点A作
,过点A作![]() 轴的平行线,分别交两条抛物线于点B、C.则以下结论:① 无论
轴的平行线,分别交两条抛物线于点B、C.则以下结论:① 无论![]() 取何值,
取何值,![]() 的值总是正数;②
的值总是正数;② ![]() ;③ 当
;③ 当![]() 时,
时,![]() ;④ 当
;④ 当![]() >
>![]() 时,0≤
时,0≤![]() <1;⑤ 2AB=3AC.其中正确结论的编号是______________.
<1;⑤ 2AB=3AC.其中正确结论的编号是______________.
【答案】①,⑤
【解析】试题分析:①∵y2=![]() (x-3)2+1﹥0,∴无论x取何值y2的值总是正的;②∵A(1,3)经过y1, ∴3=a(1+2)2-3解得a=
(x-3)2+1﹥0,∴无论x取何值y2的值总是正的;②∵A(1,3)经过y1, ∴3=a(1+2)2-3解得a=![]() ;③当x=0时,y1=
;③当x=0时,y1=![]() (0+2)2-3=-
(0+2)2-3=-![]() ,y2=
,y2=![]() (0-3)2+1=
(0-3)2+1=![]() ∴y2-y1=
∴y2-y1=![]() ④当y2﹥y1时即
④当y2﹥y1时即![]() (x+2)2-3﹤
(x+2)2-3﹤![]() (x-3)2+1.显然0≦x﹤1错误.⑤由二次函数对称性易得;
(x-3)2+1.显然0≦x﹤1错误.⑤由二次函数对称性易得;![]() (x+2)2-3=3,x1=1,x2=-5.AB=6,
(x+2)2-3=3,x1=1,x2=-5.AB=6,![]() (x-3)2+1=3,x1=1,x2="5" AC=4∴2AB=3AC. ∴只有① ⑤正确。
(x-3)2+1=3,x1=1,x2="5" AC=4∴2AB=3AC. ∴只有① ⑤正确。

练习册系列答案
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案
相关题目