Question

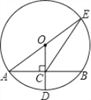
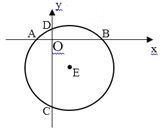
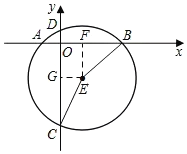
【题目】如图，在直角坐标系中，⊙E的半径为5，点E（１，-4）.

（１）求弦AB与弦CD的长；

（２）求点A，B坐标。

Answer 1

【答案】（１）AB=6 ，CD＝;（２）A（－２，０）　B（４，０）

【解析】试题分析: （1）先过E作EF⊥AB于F，作EG⊥CD于G，根据垂径定理得出BF＝AB，CG＝CD，再根据⊙E的半径为5，E（1，4），运用勾股定理求得BF和CG的长，即可得出弦AB与弦CD的长；

（2）先根据E（1，4），EF⊥AB，得出F（1，0），再根据AF＝BF＝3，即可得出OB＝1＋3＝4，AO＝31＝2，进而得到点A，B坐标．

试题解析:

（1）如图所示，过E作EF⊥AB于F，作EG⊥CD于G，

则BF＝AB，CG＝CD，

∵⊙E的半径为5，E（1，4），

∴BE＝5，EF＝4，GE＝1，

∴Rt△BEF中，BF＝＝3，

Rt△CEG中，CG＝＝2，

∴AB＝2BF＝6，CD＝2CG＝4；

（2）如图所示，∵E（1，4），EF⊥AB，

∴F（1，0），

又∵AF＝BF＝3，

∴OB＝1＋3＝4，AO＝31＝2，

∴A（2，0），B（4，0）．