题目内容
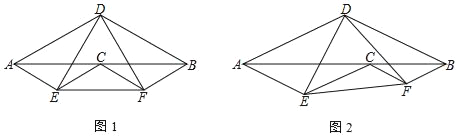
【题目】如图，点C为线段AB上一点，分别以AB、AC、CB为底作顶角为120°的等腰三角形，顶角顶点分别为D、E、F（点E、F在AB的同侧，点D在另一侧）
（1）如图1，若点C是AB的中点，则∠AED＝ ；
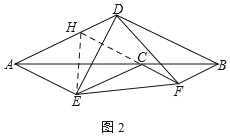
（2）如图2，若点C不是AB的中点
①求证：△DEF为等边三角形；
②连接CD，若∠ADC＝90°，AB＝3，请直接写出EF的长．
【答案】(1) 90°；(2)①见解析；②
【解析】
（1）如图1，过E作EH⊥AB于H，连接CD，设EH＝x，则AE＝2x，AH＝
x，根据等腰三角形的性质得到∠DAC＝30°，进而得到DC＝CE，又因为EH∥DC，∴∠HED＝∠EDC＝∠CED，再进一步得到∠AEH＝60°，∠HED＝30°，即可求出∠AED的大小；（2）①延长FC交AD于H，连接HE，如图2，根据等腰三角形的性质得到∠FCB＝∠FBC＝30°，∠DAB＝∠DBA＝30°，∠EAC＝∠ECA＝30°，进而得到AD∥EC∥BF，AE∥CF∥BD，所以四边形BDHF、四边形AECH是平行四边形，进而得到△AEH是等边三角形，再根据SAS判定定理得到△DHE≌△FCE，∴∠DEF＝∠CEH＝60°，∴△DEF是等边三角形；②如图3，过E作EM⊥AB于M，根据等腰三角形的性质，求出CD、CE的长，再根据勾股定理求出DE的长，因为△DEF是等边三角形，∴EF＝DE，即可得解.
（1）如图1，过E作EH⊥AB于H，连接CD，
设EH＝x，则AE＝2x，AH＝x，
∵AE＝EC，
∴AC＝2AH＝2x，
∵C是AB的中点，AD＝BD，
∴CD⊥AB，
∵∠ADB＝120°，
∴∠DAC＝30°，
∴DC＝2x，
∴DC＝CE＝2x，
∵EH∥DC，
∴∠HED＝∠EDC＝∠CED，
∵∠AEH＝60°，∠AEC＝120°，
∴∠HEC＝60°，
∴∠HED＝30°，
∴∠AED＝∠AEH＋∠HED＝90°；
故答案为：90°；
（2）①延长FC交AD于H，连接HE，如图2，
∵CF＝FB，
∴∠FCB＝∠FBC，
∵∠CFB＝120°，
∴∠FCB＝∠FBC＝30°，
同理：∠DAB＝∠DBA＝30°，∠EAC＝∠ECA＝30°，
∴∠DAB＝∠ECA＝∠FBD，
∴AD∥EC∥BF，
同理AE∥CF∥BD，
∴四边形BDHF、四边形AECH是平行四边形，
∴EC＝AH，BF＝HD，
∵AE＝EC，
∴AE＝AH，
∵∠HAE＝60°，
∴△AEH是等边三角形，
∴AE＝AH＝HE＝CE，∠AHE＝∠AEH＝60°，
∴∠DHE＝120°，
∴∠DHE＝∠FCE．
∵DH＝BF＝FC，
∴△DHE≌△FCE（SAS），
∴DE＝EF，∠DEH＝∠FEC，
∴∠DEF＝∠CEH＝60°，
∴△DEF是等边三角形；
②如图3，过E作EM⊥AB于M，
∵∠ADC＝90°，∠DAC＝30°，
∴∠ACD＝60°，
∵∠DBA＝30°，
∴∠CDB＝∠DBC＝30°，
∴CD＝BC＝
AC，
∵AB＝3，
∵AC＝2，BC＝CD＝1，
∵∠ACE＝30°，∠ACD＝60°，
∴∠ECD＝30°＋60°＝90°，
∵AE＝CE，
∴CM＝AC＝1，
∵∠ACE＝30°，
∴CE＝
，
Rt△DEC中，DE＝
＝
＝，
由①知：△DEF是等边三角形，
∴EF＝DE＝ ．
