题目内容
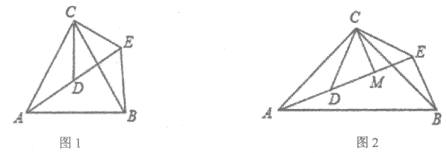
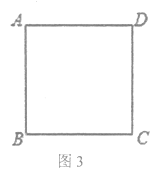
【题目】如图，小明画了一个锐角
，并作出了它的两条高
和
，两高相交于点
．小明说图形中共有两对相似三角形，他说的对吗？请你判定一下，如果正确，就其中的一对进行说理．
【答案】见解析
【解析】
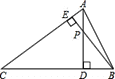
由图可知，在直角△ADC中有一个小直角△AEP，它们公共角是∠CAD，另外都有一个直角，所以运用两个角对应相等的三角形相似可得△AEP∽△ADC，在直角△BCE中有一个小直角△BDP，同理得到△BDP∽△BEC.又直角△AEP与直角△BDP，有一个对顶角相等，且都有一个直角，所以△BDP∽△AEP.
则由三角形相似的传递性可知△AEP∽△ADC∽△BDP∽△BEC，则它们两两相似，故有六对.
小明的说法不正确，因为图形中存在着6对相似三角形． 它们分别是：△AEP∽△ADC，△AEP∽△BDP，△AEP∽△BEC，△ADC∽△BDP，△ADC∽△BEC，
△BDP∽△BEC
证明：∵BE⊥AC，AD⊥BC（已知）
∴∠CEP=∠AEP=90°
又∵∠CAD=∠PAE(公共角)
∴△AEP∽△ADC（两组角对应相等的两个三角形相似）
同理可得：△BDP∽△BEC
在△BDP与△AEP中
有∠AEP=∠BDP=90°
∠APE=∠BPD（对顶角相等）
∴△BDP∽△AEP（两组角对应相等的两个三角形相似）
由相似的传递性证得：△AEP∽△ADC∽△BDP∽△BEC
故有三角形两两相似六对：
△AEP∽△ADC，△AEP∽△BDP，△AEP∽△BEC，△ADC∽△BDP，△ADC∽△BEC，
△BDP∽△BEC
练习册系列答案
名校课堂系列答案
相关题目
