题目内容
【题目】在平面直角坐标系xOy中,点A的坐标为(1,0),P是第一象限内任意一点,连接PO,PA,若∠POA=m°,∠PAO=n°,则我们把(m°,n°)叫做点P 的“双角坐标”.例如,点(1,1)的“双角坐标”为(45°,90°).
(1)点(![]() )的“双角坐标”为_____;
)的“双角坐标”为_____;
(2)若点P到x轴的距离为![]() ,则m+n的最小值为_____.
,则m+n的最小值为_____.
【答案】(60°,60°) 90
【解析】
(1)分别求出tan∠POA、tan∠PAO即可得∠POA、∠PAO的度数,从而得出答案;
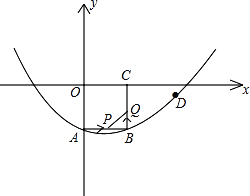
(2)根据三角形内角和定理知若要使m+n取得最小值,即∠POA+∠PAO取得最小值,则∠OPA需取得最大值,OA中点为圆心,![]() 为半径画圆,与直线y=
为半径画圆,与直线y=![]() 相切于点P,由∠OPA=∠1>∠OP′A知此时∠OPA最大,∠OPA=90°,即可得出答案.
相切于点P,由∠OPA=∠1>∠OP′A知此时∠OPA最大,∠OPA=90°,即可得出答案.
解:(1)∵P(![]() ,
,![]() ),OA=1,
),OA=1,
∴tan∠POA=![]() =
=![]() ,tan∠PAO=
,tan∠PAO=![]() =
=![]() ,
,
∴∠POA=60°,∠PAO=60°,
即点P的“双角坐标”为(60°,60°),
故答案为:(60°,60°);
(2)根据三角形内角和定理知若要使m+n取得最小值,即∠POA+∠PAO取得最小值,
则∠OPA需取得最大值,
如图,
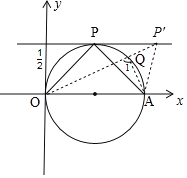
∵点P到x轴的距离为![]() ,OA=1,
,OA=1,
∴OA中点为圆心,![]() 为半径画圆,与直线y=
为半径画圆,与直线y=![]() 相切于点P,
相切于点P,
在直线y=![]() 上任取一点P′,连接P′O、P′A,P′O交圆于点Q,
上任取一点P′,连接P′O、P′A,P′O交圆于点Q,
∵∠OPA=∠1>∠OP′A,
此时∠OPA最大,∠OPA=90°,
∴m+n的最小值为90,
故答案为:90.

【题目】庐阳春风体育运动品商店从厂家购进甲,乙两种T恤共400件,其每件的售价与进货量![]() (件)之间的关系及成本如下表所示:
(件)之间的关系及成本如下表所示:
T恤 | 每件的售价/元 | 每件的成本/元 |
甲 |
| 50 |
乙 |
| 60 |
|
(1)当甲种T恤进货250件时,求两种T恤全部售完的利润是多少元;
(2)若所有的T恤都能售完,求该商店获得的总利润![]() (元)与乙种T恤的进货量
(元)与乙种T恤的进货量![]() (件)之间的函数关系式;
(件)之间的函数关系式;
(3)在(2)的条件下,已知两种T恤进货量都不低于100件,且所进的T恤全部售完,该商店如何安排进货才能使获得的利润最大?