题目内容
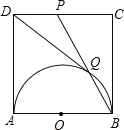
【题目】如图所示,在平面直角坐标系xOy中,正方形OABC的边长为2cm,点A、C分别在y轴的负半轴和x轴的正半轴上,抛物线y=ax2+bx+c经过点A、B和D(4,![]() ).
).
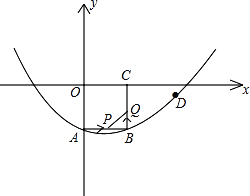
(1)求抛物线的表达式.
(2)如果点P由点A出发沿AB边以2cm/s的速度向点B运动,同时点Q由点B出发,沿BC边以1cm/s的速度向点C运动,当其中一点到达终点时,另一点也随之停止运动.设S=PQ2(cm2).
①试求出S与运动时间t之间的函数关系式,并写出t的取值范围;
②当S取![]() 时,在抛物线上是否存在点R,使得以点P、B、Q、R为顶点的四边形是平行四边形?如果存在,求出R点的坐标;如果不存在,请说明理由.
时,在抛物线上是否存在点R,使得以点P、B、Q、R为顶点的四边形是平行四边形?如果存在,求出R点的坐标;如果不存在,请说明理由.
(3)在抛物线的对称轴上求点M,使得M到D、A的距离之差最大,求出点M的坐标.
【答案】(1)抛物线的解析式为:![]() ;
;
(2)①S与运动时间t之间的函数关系式是S=5t2﹣8t+4,t的取值范围是0≤t≤1;
②存在.R点的坐标是(3,﹣![]() );
);
(3)M的坐标为(1,﹣![]() ).
).
【解析】
试题(1)设抛物线的解析式是y=ax2+bx+c,求出A、B、D的坐标代入即可;
(2)①由勾股定理即可求出;②假设存在点R,可构成以P、B、R、Q为顶点的平行四边形,求出P、Q的坐标,再分为两种种情况:A、B、C即可根据平行四边形的性质求出R的坐标;
(3)A关于抛物线的对称轴的对称点为B,过B、D的直线与抛物线的对称轴的交点为所求M,求出直线BD的解析式,把抛物线的对称轴x=1代入即可求出M的坐标.
试题解析:(1)设抛物线的解析式是y=ax2+bx+c,
∵正方形的边长2,
∴B的坐标(2,﹣2)A点的坐标是(0,﹣2),
把A(0,﹣2),B(2,﹣2),D(4,﹣![]() )代入得:
)代入得: ,
,
解得a=![]() ,b=﹣
,b=﹣![]() ,c=﹣2,
,c=﹣2,
∴抛物线的解析式为:![]() ,
,
答:抛物线的解析式为:![]() ;
;
(2)①由图象知:PB=2﹣2t,BQ=t,
∴S=PQ2=PB2+BQ2,
=(2﹣2t)2+t2,
即S=5t2﹣8t+4(0≤t≤1).
答:S与运动时间t之间的函数关系式是S=5t2﹣8t+4,t的取值范围是0≤t≤1;
②假设存在点R,可构成以P、B、R、Q为顶点的平行四边形.
∵S=5t2﹣8t+4(0≤t≤1),
∴当S=![]() 时,5t2﹣8t+4=
时,5t2﹣8t+4=![]() ,得20t2﹣32t+11=0,
,得20t2﹣32t+11=0,
解得t=![]() ,t=
,t=![]() (不合题意,舍去),
(不合题意,舍去),
此时点P的坐标为(1,﹣2),Q点的坐标为(2,﹣![]() ),
),
若R点存在,分情况讨论:
(i)假设R在BQ的右边,如图所示,这时QR=PB,RQ∥PB,
则R的横坐标为3,R的纵坐标为﹣![]() ,
,
即R(3,﹣![]() ),
),
代入![]() ,左右两边相等,
,左右两边相等,
∴这时存在R(3,﹣![]() )满足题意;
)满足题意;

(ii)假设R在QB的左边时,这时PR=QB,PR∥QB,
则R(1,﹣![]() )代入,
)代入,![]() ,
,
左右不相等,∴R不在抛物线上.(1分)
综上所述,存点一点R(3,﹣![]() )满足题意.
)满足题意.
答:存在,R点的坐标是(3,﹣![]() );
);
(3)如图,M′B=M′A,

∵A关于抛物线的对称轴的对称点为B,过B、D的直线与抛物线的对称轴的交点为所求M,
理由是:∵MA=MB,若M不为L与DB的交点,则三点B、M、D构成三角形,
∴|MB|﹣|MD|<|DB|,
即M到D、A的距离之差为|DB|时,差值最大,
设直线BD的解析式是y=kx+b,把B、D的坐标代入得: ,
,
解得:k=![]() ,b=﹣
,b=﹣![]() ,
,
∴y=![]() x﹣
x﹣![]() ,
,
抛物线![]() 的对称轴是x=1,
的对称轴是x=1,
把x=1代入得:y=﹣![]()
∴M的坐标为(1,﹣![]() );
);
答:M的坐标为(1,﹣![]() ).
).